
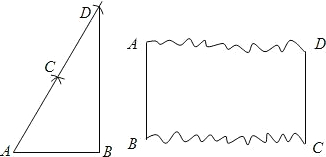
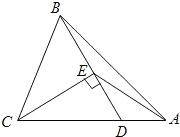
 A题解:(1)解法一:由作图知,AB=BC=CD=AB,∴BC=
A题解:(1)解法一:由作图知,AB=BC=CD=AB,∴BC= AD
AD CD,又CD=2DA,所以DE=DA.∠DAE=∠DEA=30°,CE=EA
CD,又CD=2DA,所以DE=DA.∠DAE=∠DEA=30°,CE=EA

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 某中学师生在劳动基地活动时,看到木工师傅在材料边角处画直角时,用了一种“三弧法”.
某中学师生在劳动基地活动时,看到木工师傅在材料边角处画直角时,用了一种“三弧法”.查看答案和解析>>
科目:初中数学 来源: 题型:
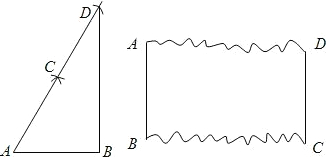
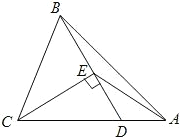
查看答案和解析>>
科目:初中数学 来源: 题型:
 某中学师生在劳动基地活动时,看到木工师傅在材料边角处画直角时,用了一种“三弧法”.方法是:
某中学师生在劳动基地活动时,看到木工师傅在材料边角处画直角时,用了一种“三弧法”.方法是:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学师生在劳动基地活动时,看到木工师傅在材料边角处画直角时,用了一种“三弧法”.方法是:
某中学师生在劳动基地活动时,看到木工师傅在材料边角处画直角时,用了一种“三弧法”.方法是:查看答案和解析>>
科目:初中数学 来源:第24章《图形的相似》中考题集(17):24.3 相似三角形(解析版) 题型:解答题


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com