
����Ŀ����ͼ����֪��ABC�У�AB=AC=6cm����B=��C��BC=4cm����DΪAB���е㣮
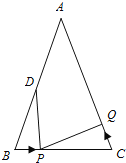
��1�������P���߶�BC����1cm/s���ٶ��ɵ�B���C�˶���ͬʱ����Q���߶�CA���ɵ�C���A�˶���
������Q���˶��ٶ����P���˶��ٶ���ȣ�����1�����BPD����CQP�Ƿ�ȫ�ȣ���˵�����ɣ�
������Q���˶��ٶ����P���˶��ٶȲ���ȣ�����Q���˶��ٶ�Ϊ����ʱ���ܹ�ʹ��BPD����CQPȫ�ȣ�
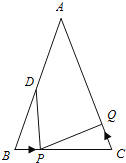
��2������Q�Ԣ��е��˶��ٶȴӵ�C��������P��ԭ�����˶��ٶȴӵ�Bͬʱ����������ʱ������ABC�����˶����� ��P���Q��һ������ABC�� �������������ں�����ֱ��д���𰸣�������д������̣�
���𰸡���1������������2������24���P���Q��һ���ڱ�AC��������
��������
�����������1���ٸ���ʱ����ٶȷֱ����������������BP��CQ��BD��PC�ߵij�������SAS�ж�����������ȫ�ȣ�
�ڸ���ȫ��������Ӧ���������̽���֮��Ĺ�ϵ���ٸ���·��=�ٶ���ʱ�乫ʽ������õ�P�˶���ʱ�䣬����õ�Q���˶��ٶȣ�
��2������������ͼ�η������֣����ڵ�Q���ٶȿ죬���ڵ�P��ǰ�ߣ�����Ҫ���һ����������Ӧ�ñȵ�P���ߵ��������ε������߳���
�⣺��1����ȫ�ȣ��������£�
��t=1�룬
��BP=CQ=1��1=1���ף�
��AB=6cm����DΪAB���е㣬
��BD=3cm��
����PC=BC��BP��BC=4cm��
��PC=4��1=3cm��
��PC=BD��
����AB=AC��
���B=��C��
���BPD�ա�CQP��
�ڼ�����BPD�ա�CQP��
��vP��vQ��
��BP��CQ��
���ߡ�BPD�ա�CQP����B=��C����BP=CP=2��BD=CQ=3��
����P����Q�˶���ʱ��t=![]() =2�룬
=2�룬
��vQ=![]() =
=![]() =1.5cm/s��
=1.5cm/s��
��2���辭��x����P���Q��һ��������
�����⣬�� 1.5x=x+2��6��
���x=24��
����P���˶���24s��1cm/s=24cm��
��24=2��12��
����P����Q��AC����������
������24���P���Q��һ���ڱ�AC��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶����ʵ��С���ѧ����ÿ����Ұ���20��ѧ������ȱ��3����ң���ÿ����Ұ���24��ѧ������ճ�һ����ң�������ѧУ���н��Ҷ��ټ䣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
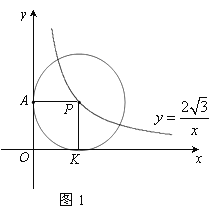
����Ŀ����ֱ������ϵxoy������֪��P�Ƿ���������![]() ͼ����һ����������PΪԲ�ĵ�Բʼ����y�����������е�ΪA��
ͼ����һ����������PΪԲ�ĵ�Բʼ����y�����������е�ΪA��
��1����ͼ1����P�˶�����x�����������е�ΪK�����ж��ı���OKPA����״����˵��������
��2����ͼ2����P�˶�����x���ཻ���轻��ΪB��C�����ı���ABCP������ʱ��
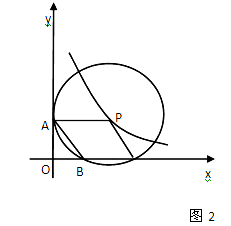
�������A��B��C��������
����P���Ҳ�ķ���������![]() ͼ���Ƿ�����ϵ�M��ʹ��MBP�������������ABCP����������������������������M���������������������˵��������
ͼ���Ƿ�����ϵ�M��ʹ��MBP�������������ABCP����������������������������M���������������������˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֻƹ�����ϣ��ֱ�д��������ͬ������������a��b��c��ʾ������ֻƹ�����������ֲ�ͬ�⣬�����ͬ������ֻƹ�������һ�������ĺ��н�����ȣ��ŻصĴ�����������2ֻƹ�����������������������.����Ϊż��ʱ����Ϊ�¼�A������Ϊ����ʱ����Ϊ�¼�B.
��1�����һ��a��b��c��ֵ��ʹ���¼�AΪ��Ȼ�������¼�.
��2�����һ��a��b��c��ֵ��ʹ���¼�B�����ĸ��ʴ����¼�A�����ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ѣ�6��(+7)+(��2)��(��9)д��ʡ�ԼӺź͵���ʽ���ʽ���ǣ� ��
A. ��6��7��2��9 B. ��6��7��2��9 C. ��6��7��2��9 D. ��6��7��2��9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ٳ�����һ����ֱ���ڵ����ϵ���ˣ�������Ȼ�´������滹ʣ��2����������������8�������Ӹպ�б����ֱ�¶˽Ӵ����棨��ͼ����
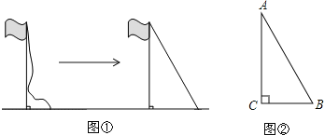
��1�����������Ķ����⣬����Ŀ������������������ͼ����Rt��ABC�� ��C=90����BC=8����____________________________.��AC�ij���
��2�����ݣ�1���е������������˵ĸ߶ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С�չ涨��һ�����������a��b=3a��2b��С�������2��5=��4�������С�ռ���2������5��= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ٽ�����ij�̳�Ϊ�������˿ͣ�����˿�������ת����ת�̣���ͼ��ʾ��ת�̱����ȵط�Ϊ20�ݣ������涨���˿�ÿ 200Ԫ����Ʒ�����ܻ��һ��ת��ת�̵Ļ��ᣮ���ת��ֹͣ��ָ�����ö���ɫ����ɫ����ɫ������ô�˿;Ϳ��Էֱ���200Ԫ��100Ԫ��50Ԫ�Ĺ���ȯ��ƾ����ȯ�����ڸ��̳����������ij�˿���300Ԫ��
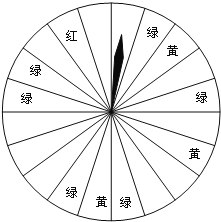
��1��������ʱ��ù���ȯ�ĸ����Ƕ��٣�
��2����������ֹ���ȯ�ĸ��������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�����D��DE��AB���E����F�ڱ�CD�ϣ�DF=BE,����AF,BF

��1����֤���ı���BFDE�Ǿ��Σ�
��2����CF=3��BF=4��DF=5����֤��AFƽ����DAB.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com