
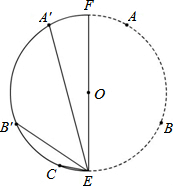
 如图,A,B,C为⊙O上相邻的三个n等分点,
如图,A,B,C为⊙O上相邻的三个n等分点, =
= ,点E在
,点E在 上,EF为⊙O的直径,将⊙O沿EF折叠,使点A与A′重合,点B与B′重合,连接EB′,EC,EA′.设EB′=b,EC=c,EA′=p.现探究b,c,p三者的数量关系:发现当n=3时,p=b+c.请继续探究b,c,p三者的数量关系:当n=4时,p=________;当n=12时,p=________.
上,EF为⊙O的直径,将⊙O沿EF折叠,使点A与A′重合,点B与B′重合,连接EB′,EC,EA′.设EB′=b,EC=c,EA′=p.现探究b,c,p三者的数量关系:发现当n=3时,p=b+c.请继续探究b,c,p三者的数量关系:当n=4时,p=________;当n=12时,p=________.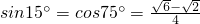 ,
,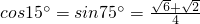 )
) b c+
b c+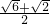 b
b ;其次,证明△ACD∽△BCE,得到
;其次,证明△ACD∽△BCE,得到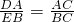 ;由EA=ED+DA,整理得到p的通项公式为:p=c+2cos
;由EA=ED+DA,整理得到p的通项公式为:p=c+2cos •b.将n=4,n=12代入,即可求得答案.
•b.将n=4,n=12代入,即可求得答案.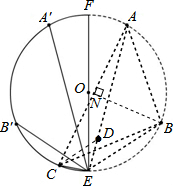 解:如解答图所示,连接AB、AC、BC.
解:如解答图所示,连接AB、AC、BC. ×
× =
= (度).
(度). •BC,
•BC, =2cos
=2cos .
. ,∠ACB=∠DCE.
,∠ACB=∠DCE. ,∠ACD=∠BCE,
,∠ACD=∠BCE,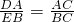 ,
, •EB=2cos
•EB=2cos •EB.
•EB. •EB.
•EB. •b.
•b. b;
b;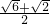 b.
b. b,c+
b,c+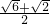 b.
b. •b,这样的结果更具普遍性;也可以按照题中要求,对于4等分或12等分的情况分别求解.
•b,这样的结果更具普遍性;也可以按照题中要求,对于4等分或12等分的情况分别求解. 

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 25、如图,以△ABC的边AB为直径的⊙O交AC边于点D,且过点D的⊙O的切线DE平分BC边,交BC于E.
25、如图,以△ABC的边AB为直径的⊙O交AC边于点D,且过点D的⊙O的切线DE平分BC边,交BC于E.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,正方形ABCDE的边长为4,E是正方形ABCD的边DC上的一点,过A作AF⊥AE,交CB延长线于点F.
如图,正方形ABCDE的边长为4,E是正方形ABCD的边DC上的一点,过A作AF⊥AE,交CB延长线于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com