
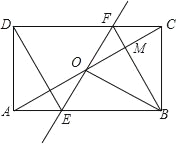
【题目】如图,矩形ABCD中,O为AC中点,过O点的直线分别于AB、CD交于E、F,连结BF交AC与点M,连结DE、BO,若∠COB=60°,FO=FC
求证:①FB⊥OC,OM=CM;
②四边形EBFD是菱形;
③MB:OE=3:2.
【答案】详见解析
【解析】
①根据已知得出△OBF≌△CBF,可求得△OBF与△CBF关于直线BF对称,进而求得FB⊥OC,OM=CM;
②先证得∠ABO=∠OBF=30°,再证得OE=OF,进而证得OB⊥EF,因为BD、EF互相平分,即可证得四边形EBFD是菱形.
③根据三角函数求得MB=![]() ,OF=
,OF=![]() ,根据OE=OF即可求得MB:OE=3:2.
,根据OE=OF即可求得MB:OE=3:2.
证明:①连接BD,
∵四边形ABCD是矩形,
∴AC=BD,AC、BD互相平分,
∵O为AC中点,
∴BD也过O点,
∴OB=OC,
∵∠COB=60°,OB=OC,
∴△OBC是等边三角形,
∴OB=BC=OC,∠OBC=60°,
在△OBF与△CBF中
 ,
,
∴△OBF≌△CBF(SSS),
∴△OBF与△CBF关于直线BF对称,
∴FB⊥OC,OM=CM;
②∵∠OBC=60°,
∴∠ABO=30°,
∵△OBF≌△CBF,
∴∠OBM=∠CBM=30°,
∴∠ABO=∠OBF,
∵AB∥CD,
∴∠OCF=∠OAE,
∵OA=OC,
易证△AOE≌△COF,
∴OE=OF,
∴OB⊥EF,
∴四边形EBFD是菱形,
③∵∠OMB=∠BOF=90°,∠OBF=30°,
∴MB=![]() ,OF=
,OF=![]() ,
,
∵OE=OF,
∴MB:OE=3:2,


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F. 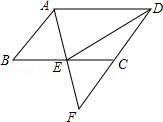
(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:边长为12的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2 , 则S1+S2的值为( ) 
A.60
B.64
C.68
D.72
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京奥运会期间,某旅行社组团去北京观看某场足球比赛,入住某宾馆.已知该宾馆一楼房间比二楼房间少5间,该旅游团有48人,若全部安排在一楼,每间住4人,房间不够,每间住5人,有房间没住满.若全部安排在二楼,每间住3人,房间不够,每间住4人,则有房间没住满.你能根据以上信息确定宾馆一楼有多少房间吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着经济的发展,能源与环境已成为人们日益关注的问题.据统计,全球每年大约会产生近3亿吨的塑料垃圾(例如平时用的矿泉水瓶子等)和约5亿吨的废钢铁(例如平时扔掉的易拉罐等),某中学为了培养学生的环保意识,开展了“环境保护,从我做起”的主题活动,七(2)班同学在活动中积极响应,在甲小区设立了回收塑料瓶和易拉罐的两个垃圾桶,班长小明对2周的收集情况进行了统计,根据下列统计表和废品收购站的价格表,解决下列问题:


(1)全班2周共收集了 斤塑料瓶,收集了 斤易拉罐.
(2)班委会决定给贫困山区的孩子们捐赠一套价值50.4元的励志丛书,你认为按照这样的收集速度,至少需要收集几周才能实现这个愿望?写出计算过程.
(3)七(1)班在乙小区也设立了塑料瓶和易拉罐的回收点,两周收集塑料瓶和易拉罐共计440个,按相同价格出售后,所得金额比七(2)班两个周的废品回收金额多1.8元,求七(1)班同学两周收集的塑料瓶和易拉罐各多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
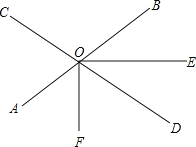
【题目】如图,直线AB、CD相交于O点,∠AOC=70,OF平分∠AOD,射线OE在∠BOD的内部(如图),∠BOE=n°.
(1)当n=30时,求∠DOE的度数;
(2)当n=35时,射线OE与OF之间有什么位置关系?
(3)若射线OD平分∠EOF,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】像(![]() +2)(
+2)(![]() ﹣2)=1、
﹣2)=1、![]()
![]() =a(a≥0)、(
=a(a≥0)、(![]() +1)(
+1)(![]() ﹣1)=b﹣1(b≥0)……两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.例如,
﹣1)=b﹣1(b≥0)……两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.例如,![]() 与
与![]() ,
,![]() +1与
+1与![]() ﹣1,2
﹣1,2![]() +3
+3![]() 与2
与2![]() ﹣3
﹣3![]() 等都是互为有理化因式.进行二次根式计算时,利用有理化因式,可以化去分母中的根号.请完成下列问题:
等都是互为有理化因式.进行二次根式计算时,利用有理化因式,可以化去分母中的根号.请完成下列问题:
(1)化简:![]() ;
;
(2)计算:![]() ;
;
(3)比较![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com