
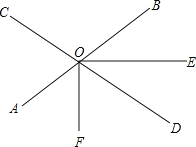
【题目】如图,直线AB、CD相交于O点,∠AOC=70,OF平分∠AOD,射线OE在∠BOD的内部(如图),∠BOE=n°.
(1)当n=30时,求∠DOE的度数;
(2)当n=35时,射线OE与OF之间有什么位置关系?
(3)若射线OD平分∠EOF,求n的值.
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD∥CO,连结CD 
(1)求证:CD是⊙O的切线;
(2)若AB=2,CD= ![]() ,求AD的长.(结果保留根号)
,求AD的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
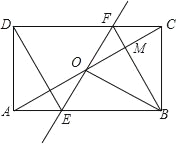
【题目】如图,矩形ABCD中,O为AC中点,过O点的直线分别于AB、CD交于E、F,连结BF交AC与点M,连结DE、BO,若∠COB=60°,FO=FC
求证:①FB⊥OC,OM=CM;
②四边形EBFD是菱形;
③MB:OE=3:2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,点E、F分别是边AD、AB的中点,连接EF.

(1)如图1,若点G是边BC的中点,连接FG,则EF与FG关系为: ;
(2)如图2,若点P为BC延长线上一动点,连接FP,将线段FP以点F为旋转中心,逆时针旋转900,得到线段FQ,连接EQ,请猜想EF、EQ、BP三者之间的数量关系,并证明你的结论;
(3)若点P为CB延长线上一动点,按照(2)中的作法,在图3中补全图形,并直接写出EF、EQ、BP三者之间的数量关系: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小武新家装修,在装修客厅时,购进彩色地砖和单色地砖共100块,共花费5600元.已知彩色地砖的单价是80元/块,单色地砖的单价是40元/块.
(1)两种型号的地砖各采购了多少块?
(2)如果厨房也要铺设这两种型号的地砖共60块,且采购地砖的费用不超过3200元,那么彩色地砖最多能采购多少块?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【新知理解】
如图①,点C在线段AB上,图中共有三条线段AB、AC和BC,若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“巧点”.
线段的中点__________这条线段的“巧点”;(填“是”或“不是”).
若AB = 12cm,点C是线段AB的巧点,则AC=___________cm;
【解决问题】
(3) 如图②,已知AB=12cm.动点P从点A出发,以2cm/s的速度沿AB向点B匀速移动:点Q从点B出发,以1cm/s的速度沿BA向点A匀速移动,点P、Q同时出发,当其中一点到达终点时,运动停止,设移动的时间为t(s).当t为何值时,A、P、Q三点中其中一点恰好是另外两点为端点的线段的巧点?说明理由

![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C、D、E在同一直线上,且AC=BD,E是线段BC的中点.
![]()
(1)点E是线段AD的中点吗?说明理由;
(2)当AD=10,AB=3时,求线段BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形.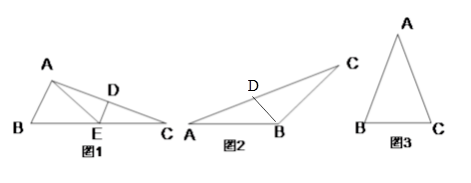
(1)如图1,△ABC中,∠B=2∠C,线段AC的垂直平分线交AC于点D,交BC于点E.
求证:AE是△ABC的一条特异线.
(2)如图2,已知BD是△ABC的一条特异线,其中∠A= ![]() ,∠ABC为钝角,求出所有可能的∠ABC的度数.
,∠ABC为钝角,求出所有可能的∠ABC的度数.
(3)如图3,△ABC是一个腰长为2的等腰锐角三角形,且它是特异三角形,若它的顶角
度数为整数,请求出其特异线的长度;若它的顶角度数不是整数,请直接写出顶角度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com