
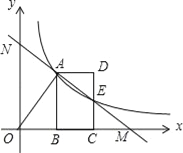
����Ŀ����ͼ��OΪԭ�㣬����������y=![]() ��x��0����ͼ���߶�OA�Ķ˵�A����AB��x���ڵ�B����A������Ϊ��2��3����
��x��0����ͼ���߶�OA�Ķ˵�A����AB��x���ڵ�B����A������Ϊ��2��3����
��1�������������Ľ���ʽΪ������
��2�����߶�AB��x��������ƽ�Ƶ��߶�DC��λ�ã�����������y=![]() ��x��0����ͼ��ǡ�þ���DC���е�E��
��x��0����ͼ��ǡ�þ���DC���е�E��
����ֱ��AE�ĺ�������ʽ��
����ֱ��AE��x�ύ�ڵ�M����y�ύ�ڵ�N������д���߶�AN���߶�ME�Ĵ�С����˵�����ɣ�
���𰸡���1�������������Ľ���ʽΪ![]() ��
��
��2����ֱ��AE�ĺ�������ʽΪy=mx+n��
���߶�AN=ME�����ɼ�������
�������������������1����A����������ʽ�������k��ֵ����2���ٸ��ݵ�E��CD���е㣬�ó���E�����꣬�������ֱ��AE�Ľ���ʽ�������ֱ��AE��������Ľ������꣬����ƽ���߷��߶γɱ��������ó����ۼ���.
�����������1������A��2��3���ڷ���������y=![]() ��x��0����ͼ���ϣ�
��x��0����ͼ���ϣ�
��k=2��3=6��
�������������Ľ���ʽΪy=![]() ��x��0����
��x��0����
�ʴ�Ϊ��y=![]() ��x��0����
��x��0����
��2����AB=CD����EΪ�߶�CD���е㣬
����E��������Ϊ![]() ��
��
��y=![]() ����y=
����y=![]() ������
������![]() =
=![]() ��
��
��ã�x=4��
����E��������4��![]() ����
����
��ֱ��AE�ı���ʽΪy=mx+n��
����A��2��3����E��4��![]() ������y=mx+n�еã�
������y=mx+n�еã�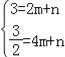 ��
��
��ã�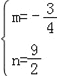 ��
��
��ֱ��AE�ı���ʽΪy=��![]() x+
x+![]() ��
��
��3��AN=ME���������£�
��y=��![]() x+
x+![]() ��y=0����0=��
��y=0����0=��![]() x+
x+![]() ��
��
��ã�x=6��
����M��������6��0����
����A��2��3����E��4��![]() ����
����
����B��2��0������C��4��0����
����B��CΪ�߶�OM�����ȷֵ㣬
��AB��CD��ƽ�Ƶ����ʣ���
����A��EΪ�߶�MN�����ȷֵ㣬
��AN=ME��


 ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������У���ȷ����( )
(1)��ȵ�Բ�Ľ����ԵĻ���ȣ�
(2)ƽ���ҵ�ֱ����ֱ���ң�
(3)������ȵ��������ǵȻ�
(4) Բ����Գ�ͼ�Σ��κ�һ��ֱ�����ǶԳ���
A. 0��B. 1��C. 2��D. 3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x��һԪ���η���(a��1)x2��x��a2��1=0��һ������0����a��ֵ�ǣ� ��
A. 1B. ��1C. 1��1D. ��1��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�� ![]()
��1��д�������ʾ������A �� B �� C �� D �� E��
��2���á�������A��B��C��D��E��ʾ��������������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com