
【题目】如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数 ![]() 的图像恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )
的图像恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( ) 
A.3
B.4
C.6
D.8
 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】移动公司推出两种话费套餐,套餐一:每月收取月租34元后,送50分钟的通话时间,超过50分钟的部分每分钟收费0.2元,并约定每月最低消费40元(当月通话费用不足40元,一律按40元收取);套餐二:每月没有最低消费,但每分钟均收取0.4元的通话费用.若分别用y1,y2(单位:元)表示套餐一、套餐二的通话费用,用x(单位:分钟)表示每个月的通话时间.
(1)分别求出y1,y2关于x的函数表达式;
(2)在如图所示的平面直角坐标系中,画出这两个函数的图象,并直接写出这两个函数图象的交点坐标;
(3)①结合图象,如何选择话费套餐才可使每月支付的通话费用较少?
②若小亮的爸爸这个月的通话费用是64元,求使用两种套餐的通话时间相差多少分钟.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为4的顶点开始,第2018次“移位”后,那么他所处的顶点的编号是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,点D为BC中点,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.求证:四边形ADCE为矩形. 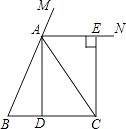
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑期临近,重庆市某中学校为了丰富学生的暑期文化生活,同时帮助孩子融洽亲子关系,增进亲子间的情感交流,计划组织学生去某景区参加为期一周的“亲子一家游”活动. 若报名参加此次活动的学生人数共有56人,其中要求参加的每名学生都至少需要一名家长陪同参加.
(1)假设参加此次活动的家长人数是参加学生人数的2倍少2人,为了此次活动学校专门为每名学生和家长购买一件T恤衫, 家长的T恤衫每购买8件赠送1件学生T恤衫(不足8件不赠送),学生T恤衫每件15元,学校购买服装的费用不超过3401元,请问每件家长T恤衫的价格最高是多少元?
(2)已知该景区的成人票价每张100元,学生票价每张50元,为了支持此次活动,该景区特地推出如下优惠活动:每张成人票价格下调a%,学生票价格下调.![]() a% 另外,经统计此次参加活动的家长人数比学生人数多a%, 参加此次活动的购买票价总费用比未优惠前减少了
a% 另外,经统计此次参加活动的家长人数比学生人数多a%, 参加此次活动的购买票价总费用比未优惠前减少了![]() a%,求a的值.
a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意解答 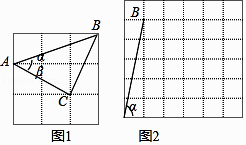
(1)如图1,如果ɑ,β都为锐角,且tanɑ= ![]() ,tanβ=
,tanβ= ![]() ,则ɑ+β=;
,则ɑ+β=;
(2)如果ɑ,β都为锐角,当tanɑ=5,tanβ= ![]() 时,在图2的正方形网格中,利用已作出的锐角ɑ,画出∠MON , 使得∠MON=ɑ﹣β.此时ɑ﹣β=度.
时,在图2的正方形网格中,利用已作出的锐角ɑ,画出∠MON , 使得∠MON=ɑ﹣β.此时ɑ﹣β=度.
查看答案和解析>>
科目:初中数学 来源: 题型:
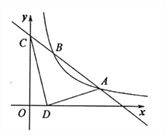
【题目】如图,已知一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点
的图像交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求反比例函数和一次函数的表达式.
(2)若在![]() 轴上有一点
轴上有一点![]() ,其横坐标是1,连接
,其横坐标是1,连接![]() 、
、![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)所示,∠AOB、∠COD都是直角.
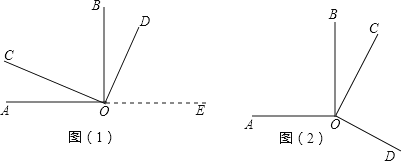
(1)试猜想∠AOD与∠COB在数量上是相等,互余,还是互补的关系.请你用推理的方法说明你的猜想是合理的.
(2)当∠COD绕着点O旋转到图(2)所示位置时,你在(1)中的猜想还成立吗?请你证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是矩形,cot∠ADB= ![]() ,AB=16.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB.
,AB=16.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB.
(1)求线段BD的长;
(2)设BE=x,△DEF的面积为y,求y关于x的函数关系式,并写出函数定义域;
(3)当△DEF为等腰三角形时,求线段BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com