
【题目】移动公司推出两种话费套餐,套餐一:每月收取月租34元后,送50分钟的通话时间,超过50分钟的部分每分钟收费0.2元,并约定每月最低消费40元(当月通话费用不足40元,一律按40元收取);套餐二:每月没有最低消费,但每分钟均收取0.4元的通话费用.若分别用y1,y2(单位:元)表示套餐一、套餐二的通话费用,用x(单位:分钟)表示每个月的通话时间.
(1)分别求出y1,y2关于x的函数表达式;
(2)在如图所示的平面直角坐标系中,画出这两个函数的图象,并直接写出这两个函数图象的交点坐标;
(3)①结合图象,如何选择话费套餐才可使每月支付的通话费用较少?
②若小亮的爸爸这个月的通话费用是64元,求使用两种套餐的通话时间相差多少分钟.

【答案】(1)y1=![]() ,y2=0.4x(x≥0);(2) (120,48);(3)①选择套餐一每月支付的通话费用较少,②两种套餐的通话时间相差40分钟.(套餐一比套餐二的通话时间多40分钟)
,y2=0.4x(x≥0);(2) (120,48);(3)①选择套餐一每月支付的通话费用较少,②两种套餐的通话时间相差40分钟.(套餐一比套餐二的通话时间多40分钟)
【解析】(1)根据两种套餐的收费标准,列出函数关系式即可;
(2)利用描点法画出图象即可;
(3)①观察图象可知,当x<120时,y2<y1,选择套餐二的通话费用较少;当x=120时,y1=y2,落在套餐费用一样;当x>120时,y2>y1,选择套餐一的通话费用较少;
②由于64>60.当y1=64时,0.2x+24=64.解得x=200;当y2=64时,0.4x=64,解得x=160,两种套餐的通话时间相差200﹣160=40(分钟).
(1)40-34=6,6÷0.2=30,50+30=80(分钟),y1=![]() ,y2=0.4x(x≥0);
,y2=0.4x(x≥0);
(2)过点A(0,40),B(80,40)画线段AB,且过B(80,40),P(120,48)画射线BP,得到折线ABP就是函数y1的图象;
过点O(0,0),点P(120,48)画射线OP得到y2的图象,两个函数的交点P的坐标(120,48);

(3)①观察图象可知,当x<120时,y2<y1,选择套餐二的通话费用较少;
当x=120时,y1=y2,落在套餐费用一样;
当x>120时,y2>y1,选择套餐一的通话费用较少;
②由于64>60.当y1=64时,0.2x+24=64.解得:x=200;
当y2=64时,0.4x=64,解得:x=160,两种套餐的通话时间相差200﹣160=40(分钟).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
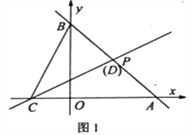
【题目】如图,直线l1经过过点P(2,2),分别交x轴、y轴于点A(4,0),B。
(1)求直线l1的解析式;
(2)点C为x轴负半轴上一点,过点C的直线l2:![]() 交线段AB于点D。
交线段AB于点D。
如图1,当点D恰与点P重合时,点Q(t,0)为x轴上一动点,过点Q作QM⊥x轴,分别交直线l1、l2于点M、N。若![]() ,MN=2MQ,求t的值;
,MN=2MQ,求t的值;
如图2,若BC=CD,试判断m,n之间的数量关系并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.

(1)数轴上点A表示的数为________.
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数是多少?
②设点A的移动距离AA′=x.
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA′的中点,点E在线段OO′上,且OE=![]() OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D是等腰直角三角形ABC斜边BC上一点(不与点B重合),连AD,线段AD绕点A逆时针方向旋转90°得到线段AE,连CE,求证:BD⊥CE. 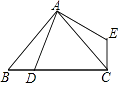
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 、
、![]() 两地相距
两地相距![]() ,甲、乙两车分别从
,甲、乙两车分别从![]() 、
、![]() 两地同时出发,甲速每小时
两地同时出发,甲速每小时![]() 千米,乙速每小时
千米,乙速每小时![]() 千米,请按下列要求列方程解题:
千米,请按下列要求列方程解题:
![]() 若同时出发,相向而行,多少小时相遇?
若同时出发,相向而行,多少小时相遇?
![]() 若同时出发,相向而行,多长时间后两车相距
若同时出发,相向而行,多长时间后两车相距![]() ?
?
![]() 若同时出发,同向而行,多长时间后两车相距
若同时出发,同向而行,多长时间后两车相距![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )

A. 13=3+10 B. 25=9+16 C. 36=15+21 D. 49=18+31
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数 ![]() 的图像恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )
的图像恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( ) 
A.3
B.4
C.6
D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com