
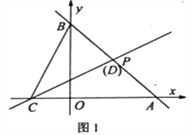
【题目】如图,直线l1经过过点P(2,2),分别交x轴、y轴于点A(4,0),B。
(1)求直线l1的解析式;
(2)点C为x轴负半轴上一点,过点C的直线l2:![]() 交线段AB于点D。
交线段AB于点D。
如图1,当点D恰与点P重合时,点Q(t,0)为x轴上一动点,过点Q作QM⊥x轴,分别交直线l1、l2于点M、N。若![]() ,MN=2MQ,求t的值;
,MN=2MQ,求t的值;
如图2,若BC=CD,试判断m,n之间的数量关系并说明理由。

【答案】(1) ![]() ;(2)①
;(2)①![]() ,
,![]() ;②
;②![]()
【解析】(1)用待定系数法求解;(2)点Q的位置有两种情况:当点Q在点A左侧,点P的右侧时![]() ;当点Q在点P的右侧时,
;当点Q在点P的右侧时,![]() .都有
.都有![]() ,再根据MN=2MQ,可求t的值;(3)由BC=CD,证△BCO≌△CDE,设C(a,0),D(4+a,-a),并代入解析式,通过解方程组可得.
,再根据MN=2MQ,可求t的值;(3)由BC=CD,证△BCO≌△CDE,设C(a,0),D(4+a,-a),并代入解析式,通过解方程组可得.
解:(1)设直线l1的解析式为y=kx+b,
直线![]() 经过点P(2,2),A(4,0),
经过点P(2,2),A(4,0),
即![]() , 解得
, 解得![]() ,
,
直线l1的解析式为y=-x+4;
(2)①∵直线l2过点P(2,2)且![]() ,
,
即直线l2:![]() ,
,
点Q(t,0),M(t,4-t),N(t,![]() ),
),
1. 当点Q在点A左侧,点P的右侧时,
![]() ,
,![]() ,
,
即![]() ,解得
,解得![]() ;
;
⒉ 当点Q在点A右侧时
![]() ,MQ=t-4,
,MQ=t-4,
即![]() ,解得t=10,
,解得t=10,
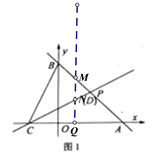
②过点D作DE⊥AC于E ,
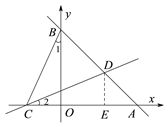
∵BC=CD,BO=OA,
∠DBC=∠1+∠ABO=∠BDC=∠2+∠DAE,
∴∠1=∠2,
∴△BCO≌△CDE,
∴OC=ED,BO=CE,
设C(a,0),D(4+a,-a),
则![]() ,
,
解得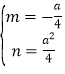 ,
,
即![]()


科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时![]() 张用A方法,其余用B方法。
张用A方法,其余用B方法。
(1)用![]() 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,E是AD的中点,延长CB到点F,使![]() ,连接BE、AF.
,连接BE、AF.
(1)完成画图并证明四边形AFBE是平行四边形;
(2)若AB=6,AD=8,∠C=60°,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E为AD上一点,FG⊥CE分别交AB、CD于F、G,垂足为O.
(1)求证:CE=FG;
(2)如图2,连接OB,若AD=3DE,∠OBC=2∠DCE。
求![]() 的值;
的值;
若AD=3,则OE的长为_________(直接写出结果).


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列判断:①单项式5×103x2的系数是5;②当x分别取2和-2时,多项式x3-2x的值互为相反数 ;③多项式﹣3a2b+7a2b2-2ab+1的次数是9;④若单项式3x2ym+2与xn-1y的和仍然是一个单项式,则m、n的值分别是-1和3;⑤几个有理数相乘,当负因数的个数为奇数时,积为负数.其中判断正确的有________________ .(将正确答案的序号填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx﹣3的对称轴为直线x=1,交x轴于A、B两点,交y轴于C点,其中B点的坐标为(3,0). 
(1)直接写出A点的坐标;
(2)求二次函数y=ax2+bx﹣3的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】移动公司推出两种话费套餐,套餐一:每月收取月租34元后,送50分钟的通话时间,超过50分钟的部分每分钟收费0.2元,并约定每月最低消费40元(当月通话费用不足40元,一律按40元收取);套餐二:每月没有最低消费,但每分钟均收取0.4元的通话费用.若分别用y1,y2(单位:元)表示套餐一、套餐二的通话费用,用x(单位:分钟)表示每个月的通话时间.
(1)分别求出y1,y2关于x的函数表达式;
(2)在如图所示的平面直角坐标系中,画出这两个函数的图象,并直接写出这两个函数图象的交点坐标;
(3)①结合图象,如何选择话费套餐才可使每月支付的通话费用较少?
②若小亮的爸爸这个月的通话费用是64元,求使用两种套餐的通话时间相差多少分钟.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com