
【题目】如图,已知抛物线y=ax2+bx﹣3的对称轴为直线x=1,交x轴于A、B两点,交y轴于C点,其中B点的坐标为(3,0). 
(1)直接写出A点的坐标;
(2)求二次函数y=ax2+bx﹣3的解析式.
【答案】
(1)解:∵抛物线y=ax2+bx﹣3的对称轴为直线x=1,交x轴于A、B两点,其中B点的坐标为(3,0),
∴A点横坐标为: ![]() =﹣1,
=﹣1,
∴A点的坐标为:(﹣1,0);
(2)解:将A(﹣1,0),B(3,0)代入y=ax2+bx﹣3得:
![]() ,
,
解得: ![]() .
.
故抛物线解析式为:y=x2﹣2x﹣3.
【解析】(1)根据抛物线的对称性直接写出点A的坐标;(2)把点A、B的坐标分别代入函数解析式列出关于a、b的方程组,通过解方程组来求它们的值.
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(1)如图①,Rt△ABC中,∠C=90°,AC=3,BC=4.点D是AB边上任意一点,则CD的最小值为 。
(2)如图②,在矩形ABCD中,AB=3,BC=4.点M、N分别在BD、BC上。求CM+MN的最小值.
(3)如图③,在矩形ABCD中,AB=3,BC=4.点E是AB边上的一点,且AE=2,点F是BC边上的任意一点。把△BEF沿EF翻折,点B对应点G,连接AG、CG.四边形AGCD的面积的最小值是 。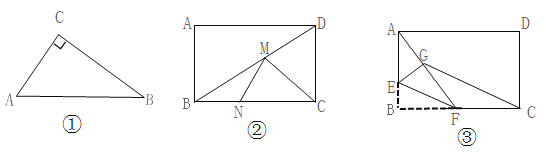
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P的坐标为(a,b),点P的“变换点”P`的坐标定义如下:当![]() 时,P`点坐标为(a,-b);当
时,P`点坐标为(a,-b);当![]() 时,P`点坐标为(b,-a)。线段l:
时,P`点坐标为(b,-a)。线段l:![]() 上所有点按上述“变换点”组成一个新的图形,若直线
上所有点按上述“变换点”组成一个新的图形,若直线![]() 与组成的新的图形有两个交点,则k的取值范围是( )
与组成的新的图形有两个交点,则k的取值范围是( )
A. ![]() B.
B. ![]() 或
或![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
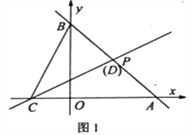
【题目】如图,直线l1经过过点P(2,2),分别交x轴、y轴于点A(4,0),B。
(1)求直线l1的解析式;
(2)点C为x轴负半轴上一点,过点C的直线l2:![]() 交线段AB于点D。
交线段AB于点D。
如图1,当点D恰与点P重合时,点Q(t,0)为x轴上一动点,过点Q作QM⊥x轴,分别交直线l1、l2于点M、N。若![]() ,MN=2MQ,求t的值;
,MN=2MQ,求t的值;
如图2,若BC=CD,试判断m,n之间的数量关系并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,学校组织学生去某景点游玩,甲旅行社说:“如果带队的一名老师购买全票,则学生享受半价优惠”; 乙旅行社说:“所有人按全票价的六折优惠”.已知全票价为a元,学生有x人,带队老师有1人.
(1)试用含a和x的式子表示甲、乙旅行社的费用;
(2)若有50名学生参加本次活动,请你为他们选择一家更优惠的旅行社.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】具备下列条件的三角形ABC中,不为直角三角形的是( )
A.∠A+∠B=∠C B.∠A=∠B=![]() ∠C
∠C
C.∠A=90°﹣∠B D.∠A﹣∠B=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第10(n是大于0的整数)个图形需要黑色棋子的个数是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.

(1)数轴上点A表示的数为________.
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数是多少?
②设点A的移动距离AA′=x.
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA′的中点,点E在线段OO′上,且OE=![]() OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )

A. 13=3+10 B. 25=9+16 C. 36=15+21 D. 49=18+31
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com