
| A. | .3或-4 | B. | .-3或4 | C. | 4 | D. | 3 |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
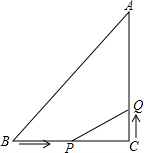 如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s速度向点c移动,同时动点Q从C出发以1cm/s的速度向点A移动,设它们的运动时间为t.
如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s速度向点c移动,同时动点Q从C出发以1cm/s的速度向点A移动,设它们的运动时间为t.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 近似数2.4×104精确到十分位 | |
| B. | 将数60340精确到千位是6.0×104 | |
| C. | 按科学记数法表示的6.05×105,其原数是60500 | |
| D. | 近似数8.1750是精确到0.001 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
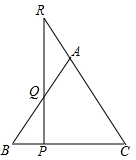 如图,P是等腰三角形ABC底边BC上的一个动点,过点P作BC的垂线,交AB于点Q,交CA的延长线于点R.请观察AR与AQ,它们有何关系?并证明你的猜想.
如图,P是等腰三角形ABC底边BC上的一个动点,过点P作BC的垂线,交AB于点Q,交CA的延长线于点R.请观察AR与AQ,它们有何关系?并证明你的猜想.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{18}-\sqrt{2}=2\sqrt{2}$ | B. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | C. | $\sqrt{12}÷\sqrt{3}={4}$ | D. | $\sqrt{5}×\sqrt{6}$=$\sqrt{11}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com