
 如图,在△A1B1C1中,已知A1B1=7,B1C1=4,A1C1=6,依次连接△A1B1C1三边中点,得△A2B2C2,再依次连接△A2B2C2的三边中点,得△A3B3C3,…,则△AnBnCn的周长=$\frac{17}{{2}^{n-1}}$.
如图,在△A1B1C1中,已知A1B1=7,B1C1=4,A1C1=6,依次连接△A1B1C1三边中点,得△A2B2C2,再依次连接△A2B2C2的三边中点,得△A3B3C3,…,则△AnBnCn的周长=$\frac{17}{{2}^{n-1}}$. 分析 根据三角形的中位线平行于第三边并且等于第三边的一半可得中点三角形的周长等于原三角形的周长的一半,然后写出前三个三角形的周长,再根据指数的变化规律写出△AnBnCn的周长即可.
解答 解:∵A1B1=7,B1C1=4,A1C1=6,
∴△A1B1C1的周长=7+4+6=17,
∵依次连接△A1B1C1三边中点,得△A2B2C2,
∴△A2B2C2的周长=$\frac{1}{2}$×17,
∵再依次连接△A2B2C2的三边中点,得△A3B3C3,
∴△A3B3C3的周长=$\frac{1}{2}$×($\frac{1}{2}$×17)=$\frac{1}{{2}^{2}}$×17,
…,
△AnBnCn的周长=$\frac{1}{{2}^{n-1}}$×17=$\frac{17}{{2}^{n-1}}$.
故答案为:$\frac{17}{{2}^{n-1}}$.
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半,三角形的周长,熟记定理并明确中点三角形的周长等于原三角形的周长的一半是解题的关键.


科目:初中数学 来源: 题型:解答题
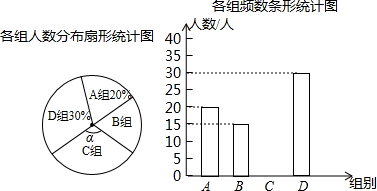 小强同学对本校学生完成家庭作业的时间进行了随机抽样调查,并绘成如下不完整的三个统计图表.
小强同学对本校学生完成家庭作业的时间进行了随机抽样调查,并绘成如下不完整的三个统计图表.| 组别 | 时间(小时) | 频数(人) | 频率 |
| A | 0≤x≤0.5 | 20 | 0.2 |
| B | 0.5<x≤1 | 15 | a |
| C | 1<x≤1.5 | 35 | 0.35 |
| D | x>1.5 | 30 | 0.3 |
| 合计 | b | 1.0 | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果AB=BC,AC⊥BD,那么四边形ABCD是菱形 | |
| B. | 如果AC=BD,AC⊥BD,那么四边形ABCD是菱形 | |
| C. | 如果AB=BC,AD∥BC,那么四边形ABCD是平行四边形 | |
| D. | 如果AO=CO,BO=DO,BC=CD,那么四边形ABCD是菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-x-2)(x-2)=x2-4 | B. | 2x(x2-2x-3)=2x3-4x2-6x | ||
| C. | (x-2y)2=x2-4xy+2y2 | D. | (x-1)(x+4)=x2-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,A、B两点在数轴上表示的数分别是a、b,则下列式子中一定成立的是( )
如图,A、B两点在数轴上表示的数分别是a、b,则下列式子中一定成立的是( )| A. | ab<2a | B. | 1-3a<1-3b | C. | |a|-|b|>0 | D. | ab>-b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com