
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊЁѕABCDЃЌABЁЮxжсЃЌAB=6ЃЌЕуAЕФзјБъЮЊЃЈ1ЃЌЉ4ЃЉЃЌЕуDЕФзјБъЮЊЃЈЉ3ЃЌ4ЃЉЃЌЕуBдкЕкЫФЯѓЯоЃЌЕуPЪЧЁѕABCDБпЩЯЕФвЛИіЖЏЕуЃЎ
ЃЈ1ЃЉШєЕуPдкБпBCЩЯЃЌPD=CDЃЌЧѓЕуPЕФзјБъЃЎ
ЃЈ2ЃЉШєЕуPдкБпABЃЌADЩЯЃЌЕуPЙигкзјБъжсЖдГЦЕФЕуQТфдкжБЯпy=xЉ1ЩЯЃЌЧѓЕуPЕФзјБъЃЎ
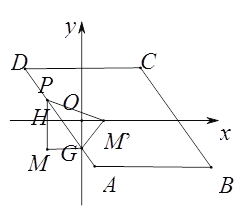
ЃЈ3ЃЉШєЕуPдкБпABЃЌADЃЌCDЩЯЃЌЕуGЪЧADгыyжсЕФНЛЕуЃЌШчЭМ2ЃЌЙ§ЕуPзїyжсЕФЦНааЯпPMЃЌЙ§ЕуGзїxжсЕФЦНааЯпGMЃЌЫќУЧЯрНЛгкЕуMЃЌНЋЁїPGMбижБЯпPGЗелЃЌЕБЕуMЕФЖдгІЕуТфдкзјБъжсЩЯЪБЃЌЧѓЕуPЕФзјБъЃЎЃЈжБНгаДГіД№АИЃЉ

ЁОД№АИЁПЃЈ1ЃЉЕуPзјБъЮЊЃЈ3ЃЌ4ЃЉЃЛЃЈ2ЃЉЕуPЕФзјБъЮЊЃЈЉ3ЃЌ4ЃЉЛђЃЈЉ1ЃЌ0ЃЉЛђЃЈ5ЃЌЉ4ЃЉЛђЃЈ3ЃЌЉ4ЃЉЃЛЃЈ3ЃЉЕуPзјБъЮЊЃЈ2ЃЌЉ4ЃЉЛђЃЈЉ![]() ЃЌ3ЃЉЛђЃЈЉ
ЃЌ3ЃЉЛђЃЈЉ![]() ЃЌ4ЃЉЛђЃЈ
ЃЌ4ЃЉЛђЃЈ![]() ЃЌ4ЃЉЃЎ
ЃЌ4ЃЉЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЕуPдкBCЩЯЃЌвЊЪЙPD=CDЃЌжЛгаPгыCжиКЯЃЛ
ЃЈ2ЃЉЪзЯШвЊЗжЕуPдкБпABЃЌADЩЯЪБЬжТлЃЌИљОнЁАЕуPЙигкзјБъжсЖдГЦЕФЕуQЁБЃЌМДЛЙвЊЯИЗжЁАЕуPЙигкxжсЕФЖдГЦЕуQКЭЕуPЙигкyжсЕФЖдГЦЕуQЁБЬжТлЃЌИљОнЙигкxжсЁЂyжсЖдГЦЕуЕФЬиеїЃЈЙигкxжсЖдГЦЪБЃЌЕуЕФКсзјБъВЛБфЃЌзнзјБъБфГЩЯрЗДЪ§ЃЛЙигкyжсЖдГЦЪБЃЌЯрЗДЃЛЃЉНЋЕУЕНЕФЕуQЕФзјБъДњШыжБЯпy=x-1ЃЌМДПЩНтД№ЃЛ
ЃЈ3ЃЉдкВЛЭЌБпЩЯЃЌИљОнЭМЯѓЃЌЕуMЗелКѓЃЌЕуMЁЏТфдкxжсЛЙЪЧyжсЃЌПЩдЫгУЯрЫЦЧѓНтЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁпCD=6ЃЌЁрЕуPгыЕуCжиКЯЃЌЁрЕуPЕФзјБъЪЧЃЈ3ЃЌ4ЃЉЃЎ
ЃЈ2ЃЉЂйЕБЕуPдкБпADЩЯЪБЃЌгЩвбжЊЕУЃЌжБЯпADЕФКЏЪ§БэДяЪНЮЊЃК![]() ЃЌЩшPЃЈaЃЌ-2a-2ЃЉЃЌЧв-3ЁмaЁм1ЃЎ
ЃЌЩшPЃЈaЃЌ-2a-2ЃЉЃЌЧв-3ЁмaЁм1ЃЎ
ШєЕуPЙигкxжсЖдГЦЕуQ1ЃЈaЃЌ2a+2ЃЉдкжБЯпy=x-1ЩЯЃЌЁр2a+2=a-1ЃЌНтЕУa=-3ЃЌДЫЪБPЃЈ-3ЃЌ4ЃЉЃЎ
ШєЕуPЙигкyжсЖдГЦЕуQ2ЃЈ-aЃЌ-2a-2ЃЉдкжБЯпy=x-1ЩЯЃЌЁр-2a-2=-a-1ЃЌНтЕУa=-1ЃЌДЫЪБPЃЈ-1ЃЌ0ЃЉЃЎ
ЂкЕБЕуPдкБпABЩЯЪБЃЌЩшPЃЈaЃЌ-4ЃЉЃЌЧв1ЁмaЁм7ЃЎ
ШєЕуPЙигкxжсЖдГЦЕуQ3ЃЈaЃЌ4ЃЉдкжБЯпy=x-1ЩЯЃЌЁр4=a-1ЃЌНтЕУa=5ЃЌДЫЪБPЃЈ5ЃЌ-4ЃЉЃЎ
ШєЕуPЙигкyжсЖдГЦЕуQ4ЃЈ-aЃЌ-4ЃЉдкжБЯпy=x-1ЩЯЃЌЁр-4=-a-1ЃЌНтЕУa=3ЃЌДЫЪБPЃЈ3ЃЌ-4ЃЉЃЎ
злЩЯЫљЪіЃЌЕуPЕФзјБъЮЊЃЈ-3ЃЌ4ЃЉЛђЃЈ-1ЃЌ0ЃЉЛђЃЈ5ЃЌ-4ЃЉЛђЃЈ3ЃЌ-4ЃЉЃЎ
ЃЈ3ЃЉвђЮЊжБЯпADЮЊy=-2x-2ЃЌЫљвдGЃЈ0ЃЌ-2ЃЉЃЎ
ЂйШчЭМЃЌЕБЕуPдкCDБпЩЯЪБЃЌПЩЩшPЃЈmЃЌ4ЃЉЃЌЧв-3ЁмmЁм3ЃЌдђПЩЕУMЁфP=PM=4+2=6ЃЌMЁфG=GM=|m|ЃЌвзжЄЕУЁїOGMЁфЁзЁїHMЁфPЃЌдђ![]() ЃЌМД
ЃЌМД![]() ЃЌдђOMЁф=
ЃЌдђOMЁф=![]() ЃЌдкRtЁїOGMЁфжаЃЌгЩЙДЙЩЖЈРэЕУЃЌ
ЃЌдкRtЁїOGMЁфжаЃЌгЩЙДЙЩЖЈРэЕУЃЌ![]() ЃЌНтЕУm=-
ЃЌНтЕУm=-![]() Лђ
Лђ![]() ЃЌдђPЃЈ-
ЃЌдђPЃЈ-![]() ЃЌ4ЃЉЛђЃЈ
ЃЌ4ЃЉЛђЃЈ![]() ЃЌ4ЃЉЃЛ
ЃЌ4ЃЉЃЛ

ЂкШчЯТЭМЃЌЕБЕуPдкADБпЩЯЪБЃЌЩшPЃЈmЃЌ-2m-2ЃЉЃЌдђPMЁф=PM=|-2m|ЃЌGMЁф=MG=|m|ЃЌвзжЄЕУЁїOGMЁфЁзЁїHMЁфPЃЌдђ![]() ЃЌМД
ЃЌМД![]() ЃЌдђOMЁф=
ЃЌдђOMЁф=![]() ЃЌдкRtЁїOGMЁфжаЃЌгЩЙДЙЩЖЈРэЕУЃЌ
ЃЌдкRtЁїOGMЁфжаЃЌгЩЙДЙЩЖЈРэЕУЃЌ![]() ЃЌећРэЕУm= -
ЃЌећРэЕУm= -![]() ЃЌдђPЃЈ-
ЃЌдђPЃЈ-![]() ЃЌ3ЃЉЃЛ
ЃЌ3ЃЉЃЛ
ШчЯТЭМЃЌЕБЕуPдкABБпЩЯЪБЃЌЩшPЃЈmЃЌ-4ЃЉЃЌДЫЪБMЁфдкyжсЩЯЃЌдђЫФБпаЮPMЁфGMЪЧе§ЗНаЮЃЌЫљвдGM=PM=4-2=2ЃЌдђPЃЈ2ЃЌ-4ЃЉЃЎ

злЩЯЫљЪіЃЌЕуPЕФзјБъЮЊЃЈ2ЃЌ-4ЃЉЛђЃЈ-![]() ЃЌ3ЃЉЛђЃЈ-
ЃЌ3ЃЉЛђЃЈ-![]() ЃЌ4ЃЉЛђЃЈ
ЃЌ4ЃЉЛђЃЈ![]() ЃЌ4ЃЉЃЎ
ЃЌ4ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїгаСНИљГЄЖШЗжБ№ЮЊ4cmКЭ9cmЕФФОАєЃЌЫћЯыдйШЁвЛИљФОАєЃЌВЂГфЗжРћгУетШ§ИљФОАєЖЄвЛИіШ§НЧаЮФОПђЃЌдђаЁУїбЁШЁЕФЕкШ§ИљФОАєГЄЖШПЩвдЪЧЃЈЁЁЁЁЃЉ
A. 5cmB. 9cmC. 13cmD. 17cm
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєA(a,b)дкЕкЖўЁЂЫФЯѓЯоЕФНЧЦНЗжЯпЩЯ,aгыbЕФЙиЯЕЪЧ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫНтЭЌбЇУЧПЮЭтдФЖСЕФЧщПіЃЌЯжЖдГѕШ§ФГАрНјааСЫЁАЮвзюЯВЛЖЕФПЮЭтЪщМЎРрБ№ЁБЕФЮЪОэЕїВщЃЌгУЁАAЁБЃЌБэЪОаЁЫЕРрЪщМЎЃЌЁАBЁББэЪОЮФбЇРрЪщМЎЃЌЁАCЁББэЪОДЋМЧРрЪщМЎЃЌЁАDЁББэЪОвеЪѕРрЪщМЎЃЎИљОнЮЪОэЕїВщЭГМЦзЪСЯЛцжЦСЫШчЯТСНЗљВЛЭъећЕФЭГМЦЭМ
ЧыИљОнЭГМЦЭМЬсЙЉЕФаХЯЂНтД№вдЯТЮЪЬтЃК

ЃЈ1ЃЉБОДЮЮЪОэЕїВщЃЌЙВЕїВщСЫЁЁ ЁЁУћбЇЩњ.
ЃЈ2ЃЉЧыВЙШЋЬѕаЮЭГМЦЭМЃЛЩШаЮЭГМЦЭМжаБэЪОЁАBЁБЕФЩШаЮдВаФНЧЮЊЁЁ ЁЁЖШЃЎ
ЃЈ3ЃЉИУАрга40ШЫЃЌЧыЭЈЙ§МЦЫуЙРМЦетИіАрЯВЛЖДЋМЧРрЪщМЎЕФДѓдМгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫСЫНтШЋаЃЦпФъМЖ300УћбЇЩњЕФЪгСІЧщПіЃЌТцРЯЪІДгжаГщВщСЫ50УћбЇЩњЕФЪгСІЧщПіЁЂеыЖдетИіЮЪЬтЃЌЯТУцЫЕЗЈе§ШЗЕФЪЧ( )
A. 300УћбЇЩњЪЧзмЬхB. УПУћбЇЩњЪЧИіЬх
C. 50УћбЇЩњЕФЪгСІЧщПіЪЧЫљГщШЁЕФвЛИібљБОD. етИібљБОШнСПЪЧ300
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=ax2+bxЉ2гыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌвбжЊAЃЈЉ1ЃЌ0ЃЉЃЌЧвtanЁЯABC=![]() .
.
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтелЪНЃЎ
ЃЈ2ЃЉдкжБЯпBCЯТЗНХзЮяЯпЩЯвЛЕуPЃЌЕБЫФБпаЮOCPBЕФУцЛ§ШЁЕУзюДѓжЕЪБЃЌЧѓДЫЪБЕуPЕФзјБъЃЎ
ЃЈ3ЃЉдкyжсЕФзѓВрХзЮяЯпЩЯгавЛЕуMЃЌТњзуЁЯMBA=ЁЯABCЃЌШєЕуNЪЧжБЯпBCЩЯвЛЕуЃЌЕБЁїMNBЮЊЕШбќШ§НЧаЮЪБЃЌЧѓЕуNЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊвЛДЮКЏЪ§y1=k1x+6гыЗДБШР§КЏЪ§y2=![]() ЯрНЛгкAЁЂBЃЌгыxжсНЛгкЕуCЃЌЙ§ЕуBзїBDЁЭxжсгкЕуDЃЌвбжЊsinЁЯDBC=
ЯрНЛгкAЁЂBЃЌгыxжсНЛгкЕуCЃЌЙ§ЕуBзїBDЁЭxжсгкЕуDЃЌвбжЊsinЁЯDBC=![]() ЃЌOCЃКCD=3ЃК1ЃЎ
ЃЌOCЃКCD=3ЃК1ЃЎ
ЃЈ1ЃЉЧѓy1КЭy2ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉСЌНгOAЃЌOBЃЌЧѓЁїAOBЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЕъОЯњвЛжжЫЋМчАќЃЌвбжЊетжжЫЋМчАќЕФГЩБОМлЮЊУПИі30дЊЃЎЪаГЁЕїВщЗЂЯжЃЌетжжЫЋМчАќУПЬьЕФЯњЪлСПyЃЈЕЅЮЛ:ИіЃЉгыЯњЪлЕЅМлxЃЈЕЅЮЛ:дЊЃЉгаШчЯТЙиЯЕЃКy=Ѓx+60ЃЈ30ЁмxЁм60ЃЉЃЎ
ЩшетжжЫЋМчАќУПЬьЕФЯњЪлРћШѓЮЊwдЊЃЎ
ЃЈ1ЃЉЧѓwгыxжЎМфЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉетжжЫЋМчАќЯњЪлЕЅМлЖЈЮЊЖрЩйдЊЪБЃЌУПЬьЕФЯњЪлРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйдЊЃП
ЃЈ3ЃЉШчЙћЮяМлВПУХЙцЖЈетжжЫЋМчАќЕФЯњЪлЕЅМлВЛИпгк48дЊЃЌИУЩЬЕъЯњЪлетжжЫЋМчАќУПЬьвЊЛёЕУ200дЊЕФЯњЪлРћШѓЃЌЯњЪлЕЅМлгІЖЈЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com