
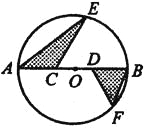
【题目】如图,半径为6cm 的⊙O中,C,D为直径AB 的三等分点,点E,F分别在AB两侧的半圆上,∠BCE =∠BDF = 60°,连结AE,BF.则图中两个阴影部分的面积和为 cm2.
【答案】![]() .
.
【解析】试题分析:作三角形DBF的轴对称图形,得到三角形AGE,三角形AGE的面积就是阴影部分的面积.
试题解析:如图作△DBF的轴对称图形△HAG,作AM⊥CG,ON⊥CE,
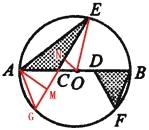
∵△DBF的轴对称图形△CAG,
由于C、D为直径AB的三等分点,则H与点C重合
∴△ACG≌△BDF,
∴∠ACG=∠BDF=60°,
∵∠ECB=60°,
∴G、C、E三点共线,
∵AM⊥CG,ON⊥CE,
∴AM∥ON,
∴![]() ,
,
在Rt△ONC中,∠OCN=60°,
∴ON=sin∠OCNOC=![]() OC,
OC,
∵OC=![]() OA=2,
OA=2,
∴ON=![]() ,
,
∴AM=![]() ,
,
∵ON⊥GE,
∴NE=GN=![]() GE,
GE,
连接OE,
在Rt△ONE中,NE=![]() ,
,
∴GE=2NE=![]() ,
,
∴S△AGE=![]() GEAM=
GEAM=![]() ,
,
∴图中两个阴影部分的面积为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)填空:与∠AOE互补的角有 ;
(2)若∠COD=30°,求∠DOE的度数;
(3)当∠AOD=α°时,请直接写出∠DOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
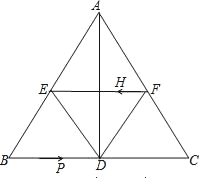
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,E点F点分别为AB,AC的中点.
(1)求证:四边形AEDF是菱形;
(2)求菱形AEDF的面积;
(3)若H从F点出发,在线段FE上以每秒2cm的速度向E点运动,点P从B点出发,在线段BC上以每秒3cm的速度向C点运动,问当t为何值时,四边形BPHE是平行四边形?当t取何值时,四边形PCFH是平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
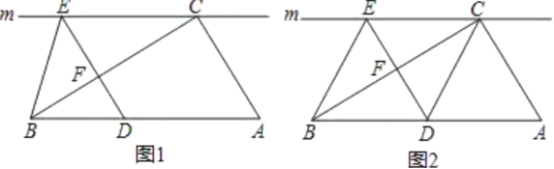
【题目】(1)(3分)如图(1),正方形AEGH的顶点E、H在正方形ABCD的边上,直接写出HD∶GC∶EB的结果(不必写计算过程);
(2)(3分)将图(1)中的正方形AEGH绕点A旋转一定角度,如图(2),求HD∶GC∶EB;
(3)(2分)把图(2)中的正方形都换成矩形,如图(3),且已知DA∶AB=HA∶AE=m: n,此时HD∶GC∶EB的值与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在
,在![]() 中,
中,![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)如图![]() ,当点
,当点![]() 是
是![]() 中点时,连接
中点时,连接![]() .
.
①四边形![]() 是什么特殊四边形?说明你的理由;
是什么特殊四边形?说明你的理由;
②当![]()
![]() 时,四边形
时,四边形![]() 是正方形.(直接写出答案)
是正方形.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.当﹣1<x<1时,化简 [x]+(x)+[x)的结果是__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.单项式 ![]() 的系数是-2,次数是3B.单项式a的系数是0,次数是0
的系数是-2,次数是3B.单项式a的系数是0,次数是0
C.![]() 是三次三项式,常数项是1D.单项式
是三次三项式,常数项是1D.单项式![]() 的次数是2,系数为
的次数是2,系数为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A,O,B依次在直线MN上.将射线OA绕点O沿顺时针方向以每秒18°的速度旋转,同时射线OB绕点O沿顺时针方向以每秒6°的速度旋转(如图2).设旋转时间为t(0≤t≤30,单位秒).
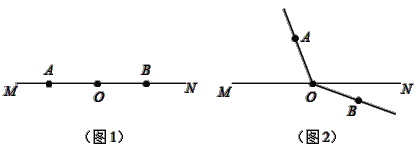
(1)当t=10时,∠AOB= °;
(2)在旋转过程中是否存在这样的t,使得射线OM是由射线OB、射线OA组成的角(指大于0°而不超过180°的角)的平分线?如果存在,请求出t的值;如果不存在,请说明理由.
(3)在运动过程中,当∠AOB=45°时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】股民李明上星期六买进春兰公司股票1000股,每股27元.下表为本周内每日该股票的涨跌情况(单位:元)(注:本周一股票涨跌是在上周六的基础上,用正数记股价比前一日上升数,用负数记股价比前一日下降数)
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
每股涨跌 | +4 | +4.5 | -1 | -2.5 | -6 | +2 |
(1)星期三收盘时,每股是多少元?
(2)本周内最高价是每股多少元?最低价每股多少元?
(3)己知李明买进股票时付了0.15%的手续费,卖出时需付成交额0.15%的手续费和0.1%的交易税,如果李明在星期六收盘前将全部股票卖出,他的收益情况如何?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com