
【题目】如图1,点A,O,B依次在直线MN上.将射线OA绕点O沿顺时针方向以每秒18°的速度旋转,同时射线OB绕点O沿顺时针方向以每秒6°的速度旋转(如图2).设旋转时间为t(0≤t≤30,单位秒).
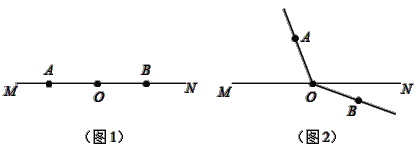
(1)当t=10时,∠AOB= °;
(2)在旋转过程中是否存在这样的t,使得射线OM是由射线OB、射线OA组成的角(指大于0°而不超过180°的角)的平分线?如果存在,请求出t的值;如果不存在,请说明理由.
(3)在运动过程中,当∠AOB=45°时,求t的值.
【答案】(1)60°;(2)t=![]() ;(3)t=
;(3)t=![]() 或
或![]() .
.
【解析】
(1)当t=10时,∠AOM=18°×10=180°,即OA与ON重合,故
∠AOB=∠BON=60°.
(2)求OA追上OB的大致时刻,得到OM平分∠AOB时的图形,用t表示此时
∠AOM与∠BOM的度数,列方程即可求t.
(3)OA、OB都是顺时针旋转,可理解为初始路程差为180°的追及问题:
当∠AOB第一次达到45°时,OA差300追上OB,路程差为(180-45)°即得18t-6t=180-45;当∠AOB第二次达到45°时,OA追上OB且超过45°,路程差为(180+45)°;
当∠AOB第三次达到45°时,OA再走一圈差45°追上OB,路程差为多转了(180+360-45)°,此时求出的t大于30故不需再求.
(1)当t=10时,∠AOM=18°×10=180°,∠BON=6°×10=60°
∠AOB=180°-∠AOM+∠BON=60°故答为60°.
(2)存在满足条件的t值.
OA旋转一周所需时间为:360°÷18=20秒,
此时∠BON=6°×20=120°,即OA已经旋转过OB的位置,
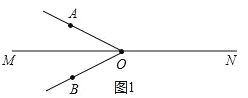
若OM平分∠AOB且0°<∠AOB<180°位置如图1,
∴∠AOM=(18t-360)°,∠BOM=(180-6t)°
∴18t-360=180-6t,解得t=![]() ,
,
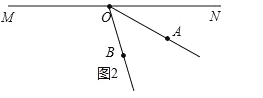
(3)如图2,当∠AOB第一次达到45°时,OA比OB多转了(180-45)°
得18t-6t=180-45,解得t=![]() ,
,
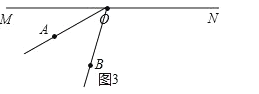
如图3,当∠AOB第二次达到45°时,OA比OB多转了(180+45)°,
得18t-6t=180+45,解得t=![]() ,
,
当∠AOB第三次达到45°时,OA比OB多转了(180+360-45)°,
得18t-6t=180+360-45,解得t= ![]() 大于30,不合题意,
大于30,不合题意,
综上所述,当∠AOB=45°时,t=![]() 或
或![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFMN的一边MN在边BC上,顶点E、F分别在AB、AC上,其中BC=24cm,高AD=12cm.
(1)求证:△AEF∽△ABC:
(2)求正方形EFMN的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
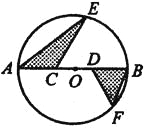
【题目】如图,半径为6cm 的⊙O中,C,D为直径AB 的三等分点,点E,F分别在AB两侧的半圆上,∠BCE =∠BDF = 60°,连结AE,BF.则图中两个阴影部分的面积和为 cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进枇杷20吨,桃子12吨.现计划租用甲、乙两种货车共8辆将这批水果运回,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.
(1)如何安排甲、乙两种货车可一次性地运到?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果商场应选择哪种方案,使运输费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时![]() 张用A方法,其余用B方法。
张用A方法,其余用B方法。
(1)用![]() 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
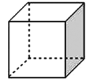
【题目】用一个平面去截正方体(如图),下列关于截面(截出的面)形状的结论:
①可能是锐角三角形;②可能是钝角三角形;
③可能是长方形;④可能是梯形.
其中正确结论的是______(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
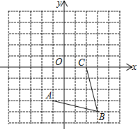
【题目】如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度
(1) 请在所给的网格内画出以线段AB、BC为边的□ABCD并写出点D的坐标_________
(2) 线段BD的长为_____________
(3) 点C到AB的距离为_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家今年种植的“红灯”樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行跟踪记录,并将记录情况绘成图象,日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图1所示,樱桃价格z(单位:元/千克)与上市时间x(单位:天)的函数关系式如图2所示.

(1)观察图象,直接写出日销售量的最大值;
(2)求小明家樱桃的日销售量y与上市时间x的函数解析式;
(3)试比较第10天与第12天的销售金额哪天多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com