
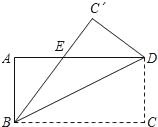
【题目】如图,将矩形ABCD沿着对角线BD折叠,使点C落在C'处,BC'交AD于E,AD=8,AB=4,
(1)判断△BDE的形状并说明理由;
(2)求△DEC'的面积.
【答案】(1)△BDE是等腰三角形,理由见解析;(2)S△DEC'=6.
【解析】整体分析:
(1)由折叠得∠DBC=∠DBE,由AD∥BC得∠ADB=∠DBC,从而有∠DBE=∠ADB;(2)在Rt△ABE中,用勾股定理列方程求出AE,则可得△ABE,△EBD的面积,即可求解.
解:(1)△BDE是等腰三角形,理由如下:
由折叠可知,∠CBD=∠EBD,
∵AD∥BC,
∴∠CBD=∠EDB,
∴∠EBD=∠EDB,
∴BE=DE,
即△BDE是等腰三角形;
(2)设DE=x,则BE=x,AE=8﹣x,
在Rt△ABE中,由勾股定理得:AB2+AE2=BE2即42+(8﹣x)2=x2,
解得:x=5,
所以S△BDE=![]() DE×AB=
DE×AB=![]() ×5×4=10,
×5×4=10,
所以S△DEC′=S△BCD′﹣S△BDE=![]() ×8×4-10=6.
×8×4-10=6.
所以△DEC'的面积为6.


科目:初中数学 来源: 题型:
【题目】为了考察甲、乙两种小麦的长势,分别从中抽出20株测得其高度,并求得它们的方差分别为S甲2=3.6,S乙2=15.8,则_______种小麦的长势比较整齐.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“美丽乡村”评选活动中,某乡镇7个村的得分如下:98,90,88,96,92,96,86,这组数据的中位数和众数分别是( )
A. 90,96 B. 92,96 C. 92,98 D. 91,92
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)平面上不重合的两点确定一条直线,不同三点最多可确定3条直线,若平面上不同的n个点最多可确定28条直线,则n的值是( )
A. 6 B. 7 C. 8 D. 9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com