Question

16．如图，已知A、B两点的坐标分别为A（$2\sqrt{3}$，0），B（0，2），点P是△AOB外接圆上的一点，且∠AOP=45°．

（1）如图1，求点P的坐标；
（2）如图2，连接BP，AP，在PB上任取一点E，连AE，将线段AE绕A点顺时针旋转90°到AF，连BF，交AP于点G，当E在线段BP上运动时（不与B，P重合），求$\frac{BE}{PG}$的值；
（3）如图3，点Q是弧$\widehat{AP}$上一动点（不与A、P重合），连接PQ、AQ、BQ，求：$\frac{BQ-AQ}{PQ}$的值．

Answer 1

分析 （1）作辅助线，构建直角三角形，证明△ABP和△OHP是等腰直角三角形，根据A（$2\sqrt{3}$，0），B（0，2），表示OA=2$\sqrt{3}$，OB=2，利用勾股定理求AB、AP，设OH=a，根据勾股定理列方程得出结论；
（2）作垂线PK，证明△AFK≌△EAP和△GFK≌△GBP，得PG=GK=$\frac{1}{2}$PK=$\frac{1}{2}$BE，代入可得结论；
（3）作辅助线，构建全等三角形，根据三个角是直角的四边形是矩形，先证明四边形PDQE是矩形，证明△PBD≌△PAE，得这个矩形为正方形，则DQ=QE，表示BQ-AQ=2QD，再由等腰直角△PQD得：PQ=$\sqrt{2}$DQ，代入计算即可．

解答 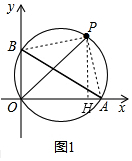解：（1）如图1，过P作PH⊥x轴于H，连接PA、PB，
∵∠AOB=90°，
∴AB为△AOB外接圆的直径，
∴∠BPA=90°，
∵A（$2\sqrt{3}$，0），B（0，2），
∴OA=2$\sqrt{3}$，OB=2，
由勾股定理得：AB=$\sqrt{O{B}^{2}+O{A}^{2}}$=$\sqrt{{2}^{2}+（2\sqrt{3}）^{2}}$=4，
∵∠AOP=45°，
∴∠ABP=∠AOP=45°，
∴△ABP和△OHP是等腰直角三角形，
∴PA=$\frac{AB}{\sqrt{2}}$=$\frac{4}{\sqrt{2}}$=2$\sqrt{2}$，OH=PH，
设OH=a，则PH=a，AH=2$\sqrt{3}$-a，
在Rt△AHP中，AP²=AH²+PH²，
（2$\sqrt{2}$）²=（2$\sqrt{3}$-a）²+a²，
解得：a₁=$\sqrt{3}$+1，a₂=$\sqrt{3}$-1（舍），
∴P（$\sqrt{3}$+1，$\sqrt{3}$+1）；
（2）如图2，过F作FK⊥AP于K，
∴∠PAF+∠AFK=90°，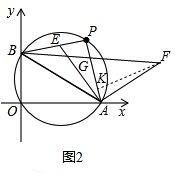
由旋转得：∠EAF=90°，EA=AF，
∴∠EAF+∠PAF=90°，
∴∠AFK=∠EAP，
∵∠APE=∠AKF=90°，
∴△AFK≌△EAP，
∴AK=PE，FK=AP=BP，
∵∠BPG=∠GKF=90°，∠BGP=∠FGK，
∴△GFK≌△GBP，
∴PG=GK=$\frac{1}{2}$BK，
∵BP=AP，PE=AK，
∴PB-PE=AP-AK，
即BE=PK，
∴PG=$\frac{1}{2}$BE，
∴BE=2PG，
∴$\frac{BE}{PG}$=2；
（3）如图3，过P作PD⊥BQ于Q，过P作PE⊥AQ，交AQ 的延长线于E，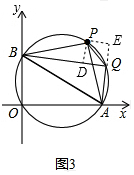
则∠PDQ=∠PEQ=90°，
∵AB是直径，
∴∠AQB=90°，
∴四边形PDQE是矩形，
由（1）得AP=BP，
∵∠PBQ=∠PAQ，∠PDB=∠PEA=90°，
∴△PBD≌△PAE，
∴BD=AE，PD=PE，
∴矩形PDEQ为正方形，
∴DQ=QE，
∴BD=AE=AQ+QE=DQ+AQ，
∴BQ-AQ=BD+DQ-AQ=DQ+AQ+DQ-AQ=2DQ，
∵∠PQB=∠PAB=45°，
∴△PDQ是等腰直角三角形，
∴PQ=$\sqrt{2}$DQ，
∴$\frac{BQ-AQ}{PQ}$=$\frac{2DQ}{\sqrt{2}DQ}$=$\sqrt{2}$．

点评 本题是圆的综合题，难度适中，考查了圆中有关的性质：①90°的圆周角所对的弦是直径，反之，直径所对的圆周角是直角，②同弧所对的圆周角相等，还考查了三角形全等的性质和判定，本题的关键是作辅助线，构建全等三角形．