
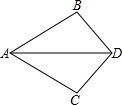
 如图,已知AB=AC,请你添加一个条件:BD=CD,使△ABD≌△ACD.
如图,已知AB=AC,请你添加一个条件:BD=CD,使△ABD≌△ACD. 分析 根据题意可得:AD=AD,再有条件∠BAD=∠CAD,可添加BD=CD,根据SAS可判断△ADB≌△ACD.
解答 解:添加的条件是:BD=CD,
理由:∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△ABD和△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAD}\\{AD=AD}\end{array}\right.$,
∴△ABD≌△ACD(SAS).
故答案为:BD=CD,(或∠BAC=∠CAD)
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


科目:初中数学 来源: 题型:解答题
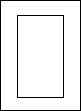 小明看自己设计一个画轴,如图,画轴长为20m,宽为10m,正中央是一个与整个画轴长、宽比例相同的矩形,如果四周边衬所占面积是整个画轴面积的$\frac{16}{25}$,且上、下边衬等宽.左、右边衬等宽.求左、右边衬的宽.
小明看自己设计一个画轴,如图,画轴长为20m,宽为10m,正中央是一个与整个画轴长、宽比例相同的矩形,如果四周边衬所占面积是整个画轴面积的$\frac{16}{25}$,且上、下边衬等宽.左、右边衬等宽.求左、右边衬的宽.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=2,b=$\sqrt{5}$,c=2$\sqrt{3}$,d=$\sqrt{3}$ | B. | a=$\sqrt{2}$,b=2,c=1,d=$\sqrt{2}$ | ||
| C. | a=4,b=6,c=5,d=10 | D. | a=12,b=8,c=15,d=11 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
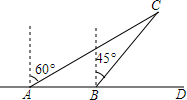 如图,上午9时,一条船从A处出发,以每小时40海里的速度向正东方向航行,9时30分到达B处,从A、B两处分别测得小岛C在北偏东60°和北偏东45°方向上,已知小岛C周围方圆30海里的海域内有暗礁.该船若继续向东方向航行,有触礁的危险吗?并说明理由.
如图,上午9时,一条船从A处出发,以每小时40海里的速度向正东方向航行,9时30分到达B处,从A、B两处分别测得小岛C在北偏东60°和北偏东45°方向上,已知小岛C周围方圆30海里的海域内有暗礁.该船若继续向东方向航行,有触礁的危险吗?并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两个有理数的和一定大于其中任何一个加数 | |
| B. | 零减去一个数仍得这个数 | |
| C. | 两个有理数的差一定小于被减数 | |
| D. | 零加上一个数仍得这个数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果k=0,则k$\overrightarrow{a}$=0 | B. | 如果m,n为实数,则m(n$\overrightarrow{a}$)=(mn)$\overrightarrow{a}$ | ||
| C. | 如果m,n为实数,则(m+n)$\overrightarrow{a}$=m$\overrightarrow{a}$+n$\overrightarrow{a}$ | D. | 如果m为实数,则m($\overrightarrow{a}+\overrightarrow{b}$)=m$\overrightarrow{a}$+n$\overrightarrow{b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com