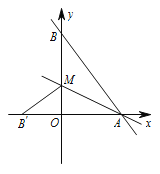
【题目】直线 
与 
轴、 
轴分别交于点 
和点 
，
是 
上的一点，若将 
沿 
折叠，点 恰好落在 轴上的点 
处，则直线 的解析式为________________．
科目：初中数学 来源： 题型：
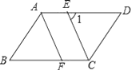
【题目】如图，在ABCD中，CE平分∠BCD，且交AD于点E，AF∥CE，且交BC于点F．
（1）求证：△ABF≌△CDE；
（2）如图，若∠B=52°，求∠1的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某面粉厂从生产的袋装面粉中抽出样品20袋，检测每袋的质量是否符合标准，超过、不足的部分分别用正、负数来表示，记录如下表：
与标准质量的差值（单位：千克） | －0.3 | －0.2 | －0.1 | 0 | 0.1 | 0.2 |
袋数 | 3 | 2 | 4 | 6 | 3 | 2 |
（1）这批样品中最多的一袋比最少的一袋多多少千克？
（2）这20袋面粉的总质量比标准的质量多（或少）多少千克？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】几何计算：
如图，已知∠AOB=40°，∠BOC=3∠AOB，OD平分∠AOC，求∠COD的度数．
解：因为∠BOC=3∠AOB，∠AOB=40°
所以∠BOC=__________°
所以∠AOC=__________ + _________
=__________° + __________°
=__________°
因为OD平分∠AOC
所以∠COD=
__________=__________°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知A，O，B三点在同一条直线上，OD平分∠AOC，OE平分∠BOC．
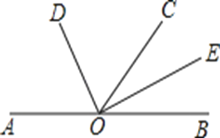
（1）若∠BOC=62°，求∠DOE的度数；
（2）若∠BOC=α，求∠DOE的度数；
（3）通过（1）(2)的计算，你能总结出什么结论,直接简写出来，不用说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】学校初一年级参加社会实践课，报名第一门课的有x人，第二门课的人数比第一门课的
少20人，现在需要从报名第二门课的人中调出10人学习第一门课，那么用含x的式子解答下题．
（1）报两门课的共有多少人？
（2）调动后，报名第一门课比报名第二门课多多少人？计算出代数式后，请选择一个你觉得合适的x值代入，并求出具体人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将
的边
绕点
顺时针旋转
得到
，边
绕点逆时针旋转
得到
，
，连接
，作
的中线
．
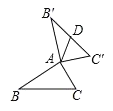
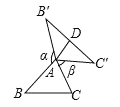
图① 图② 图③
（初步感知）
(1)如图①，当
，
时，的长为 ；
（探究运用）
(2)如图②，为任意三角形时，猜想与
的数量关系，并证明．
（应用延伸）
(3)如图③，已知等腰
，
，延长到
，延长
到
，使
，将
绕点
顺时针旋转一周得到
，连接
、
，若
，求的长度(用含
、
的代数式表示)．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】
朗读者
自开播以来，以其厚重的文化底蕴和感人的人文情怀，感动了数以亿计的观众，岳池县某中学开展“朗读”比赛活动，九年级
、
班根据初赛成绩，各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩
满分为100分
如图所示．
平均数 | 中位数 | 众数 | |
九 | 85 | 85 | |
九 | 80 |
根据图示填写表格；
结合两班复赛成绩的平均数和中位数，分析哪个班级的复赛成绩较好；
如果规定成绩较稳定班级胜出，你认为哪个班级能胜出？说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
