练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知A，O，B三点在同一条直线上，OD平分∠AOC，OE平分∠BOC．

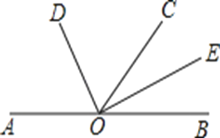
    （1）若∠BOC=62°，求∠DOE的度数；

    （2）若∠BOC=α，求∠DOE的度数；

    （3）通过（1）(2)的计算，你能总结出什么结论,直接简写出来，不用说明理由.

    【答案】（1）90°；（2）90°；（3）∠DOE=90°.

    【解析】

    （1）OD平分∠AOC，OE平分∠BOC，得出∠DOE（∠BOC+∠COA），代入数据求得问题；

    （2）利用（1）的结论，把∠BOC=a°，代入数据求得问题；

    （3）根据（1）（2）即可得出结论．

    （1）∵OD平分∠AOC，OE平分∠BOC，∴∠DOC∠AOC，∠COE∠BOC，∴∠DOE=∠DOC+∠COE（∠BOC+∠COA）（62°+180°﹣62°）=90°；

    （2）∠DOE═（∠BOC+∠COA）（a°+180°﹣a°）=90°；

    （3）由（1）（2）可得：∠DOE=90°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

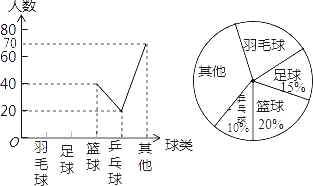
    【题目】某中学在实施快乐大课间之前组织过“我最喜欢的球类”的调查活动，每个学生仅选择一项，通过对学生的随机抽样调查得到一组数据，如图是根据这组数据绘制成的不完整统计图．

    （1）求出被调查的学生人数；

    （2）把折线统计图补充完整；

    （3）小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球，当时只有一副空球桌，他们只能选两人打第一场．如果确定小亮打第一场，其余三人用“手心、手背”的方法确定谁获胜谁打第一场若三人中有一人出的与其余两人不同则获胜；若三人出的都相同则平局．已知大刚出手心，请用树状图分析大刚获胜的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，双曲线y＝经过Rt△BOC斜边上的点A，且满足，与BC交于点D，S△BOD＝21，求：

    （1）S△BOC

    （2）k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)阅读下面材料：

    点A、B在数轴上分别表示实数a、b, A、B两点之间的距离表示为AB,若a≥b，则 | a－b | = a－b；若a < b，则 | a－b | = b－a,当A、B两点中有一点在原点时, 不妨设点A在原,

    如图甲, AB = OB =∣b∣=∣a b∣;当A、B两点都不在原点时,

    ① 如图乙,点A、B都在原点的右边,AB=OBOA=|b||a|=ba =|ab |;

    ②如图丙,点A、B都在原点的左边, AB = OB OA =|b||a|= b (a) = |ab|;

    ③如图丁,点A、B在原点的两边AB=OA+OB=|a|+|b|=a+(b) =|ab|.

    综上所述,数轴上A、B两点之间的距离AB=∣ab∣.

    (2)回答下列问题：

    ①数轴上表示1和3的两点之间的距离是______,数轴上表示1和3的两点之间的距离是______;

    ②数轴上表示x和1的两点分别是点A和B，则A、B之间的距离表示为______,如果AB=2，那么x =________ ;

    ③当代数式∣x +1∣+∣x 3∣取最小值时,相应的x的取值范围是_________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

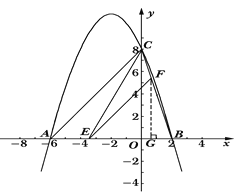
    【题目】已知：二次函数的图象与x轴交于A、B两点，与y轴交于点C，其中点B在x轴的正半轴上，点C在y轴的正半轴上，线段OB、OC的长（OB＜OC）是方程x2－10x＋16＝0的两个根，且A点坐标为（－6，0）．

    （1）求此二次函数的表达式；

    （2）若点E是线段AB上的一个动点（与点A、点B不重合），过点E作EF∥AC交BC于点F，连接CE，设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式，并写出自变量m的取值范围；

    【答案】（1）y＝－x2－x＋8（2）

    【解析】试题分析:(1)求出一元二次方程的两根即可求出两点坐标,把B、C两点坐标代入二次函数的解析式就可解答；

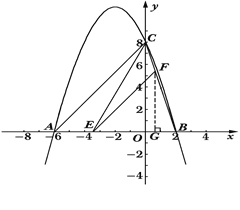
    (2)过点F作FG⊥AB，垂足为G，由EF∥AC，得△BEF∽△BAC，利用相似比求EF，利用sin∠FEG=sin∠CAB求FG，根据S=S△BCE-S△BFE，求S与m之间的函数关系式.

    解:(1）解方程x2－10x＋16＝0得x1＝2，x2＝8

    ∴B（2，0）、C（0，8）

    ∴所求二次函数的表达式为y＝－x2－x＋8

    （2）∵AB＝8，OC＝8，依题意，AE＝m，则BE＝8－m，

    ∵OA＝6，OC＝8， ∴AC＝10.

    ∵EF∥AC, ∴△BEF∽△BAC.

    ∴＝.　　即＝. ∴EF＝.

    过点F作FG⊥AB，垂足为G，

    则sin∠FEG＝sin∠CAB＝.∴＝.　

    ∴FG＝·＝8－m.

    ∴S＝S△BCE－S△BFE

    ＝

    （0＜m＜8）

    点睛:本题考查了一元二次方程的解法，待定系数法求函数关系系，相似三角形的判定与性质,span>锐角三角函数的定义，割补法求图形的面积，熟练掌握待定系数法求二次函数关系式、相似三角形的判定与性质是解答本题的关键.

    【题型】解答题
    【结束】
    23

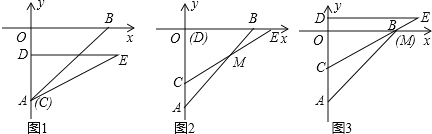
    【题目】如图（1），在平面直角坐标系中，点A（0，﹣6），点B（6，0）．Rt△CDE中，∠CDE=90°，CD=4，DE=4，直角边CD在y轴上，且点C与点A重合．Rt△CDE沿y轴正方向平行移动，当点C运动到点O时停止运动．解答下列问题：

    （1）如图（2），当Rt△CDE运动到点D与点O重合时，设CE交AB于点M，求∠BME的度数．

    （2）如图（3），在Rt△CDE的运动过程中，当CE经过点B时，求BC的长．

    （3）在Rt△CDE的运动过程中，设AC=h，△OAB与△CDE的重叠部分的面积为S，请写出S与h之间的函数关系式，并求出面积S的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

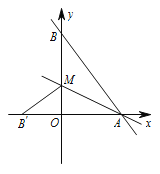
    【题目】直线 与 轴、 轴分别交于点 和点 ， 是 上的一点，若将 沿 折叠，点 恰好落在 轴上的点 处，则直线 的解析式为________________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校计划在总费用元的限额内，租用汽车送名学生和名教师集体参加校外实践活动，为确保安全，每辆汽车上至少要有名教师．现有甲、乙两种大客车，它们的载客量和租金如下表所示．

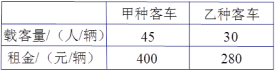
    （1）根据题干所提供的信息，确定共需租用多少辆汽车？

    （2）请你给学校选择一种最节省费用的租车方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

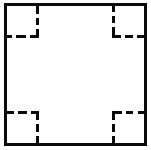
    【题目】如图，把一边长为厘米的正方形纸板的四个角各剪去一个边长为厘米的小正方形，然后把它折成一个无盖纸盒.

    （1）该纸盒的高是 厘米，底面积是 平方厘米；

    （2）该纸盒的全面积（外表面积）为 平方厘米；

    （3）为了使纸盒底面更加牢固且达到废物利用的目的，现考虑将剪下的四个小正方形平铺在盒子的底面，要求既不重叠又恰好铺满（不考虑纸板的厚度），求此时与之间的倍数关系.（直接写出答案即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在矩形ABCD中，AD=3，CD=4，点E在CD上，且DE=1．

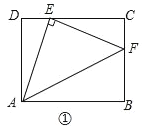
    （1）感知：如图①，连接AE，过点E作EF丄AE，交BC于点F，连接AE，易证：△ADE≌△ECF（不需要证明）；

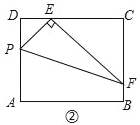
    （2）探究：如图②，点P在矩形ABCD的边AD上（点P不与点A、D重合），连接PE，过点E作EF⊥PE，交BC于点F，连接PF．求证：△PDE和△ECF相似；

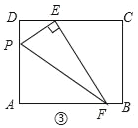
    （3）应用：如图③，若EF交AB于点F，EF丄PE，其他条件不变，且△PEF的面积是6，则AP的长为_____．

    查看答案和解析>>

    同步练习册答案