
【题目】(1)阅读下面材料:
点A、B在数轴上分别表示实数a、b, A、B两点之间的距离表示为AB,若a≥b,则 | a-b | = a-b;若a < b,则 | a-b | = b-a,当A、B两点中有一点在原点时, 不妨设点A在原,
如图甲, AB = OB =∣b∣=∣a b∣;当A、B两点都不在原点时,
![]()
① 如图乙,点A、B都在原点的右边,AB=OBOA=|b||a|=ba =|ab |;
![]()
②如图丙,点A、B都在原点的左边, AB = OB OA =|b||a|= b (a) = |ab|;
![]()
③如图丁,点A、B在原点的两边AB=OA+OB=|a|+|b|=a+(b) =|ab|.
![]()
综上所述,数轴上A、B两点之间的距离AB=∣ab∣.
(2)回答下列问题:
①数轴上表示1和3的两点之间的距离是______,数轴上表示1和3的两点之间的距离是______;
②数轴上表示x和1的两点分别是点A和B,则A、B之间的距离表示为______,如果AB=2,那么x =________ ;
③当代数式∣x +1∣+∣x 3∣取最小值时,相应的x的取值范围是_________.
【答案】①2;4②|x+1|,1或-3;③-1≤x≤3.
【解析】
①直接根据数轴上A、B两点之间的距离|AB|=|a-b|.代入数值运用绝对值即可求任意两点间的距离;②直接根据数轴上A、B两点之间的距离|AB|=|a-b|,表示AB两点距离,再结合数轴分类讨论求x的值;③根据题意,利用分类讨论的数学思想可以解答本题.
解:①数轴上表示1和3的两点之间的距离是|1-3|=2,数轴上表示1和-3的两点之间的距离是|1-(-3)|=4.故答案为:2;4.
②数轴上表示x和-1的两点A和B之间的距离是|x-(-1)|=|x+1|,
如果|AB|=2,那么x为1或-3; 故答案为:|x+1|,1或-3;
③|x+1|+|x-3|有最小值,最小值是4,取值范围是 -1≤x≤3.
理由:当x>3时,|x+1|+|x-3|=x+1+x-3=2x-4>4,
当-1≤x≤3时,|x+1|+|x-3|=x+1+3-x=4,
当x<-1时,|x+1|+|x-3|=-x-1+3-x=2-2x>4,
故|x+1|+|x-3|有最小值,最小值是4,取值范围-1≤x≤3.


科目:初中数学 来源: 题型:
【题目】为了预防流感,某学校在星期天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(小时)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据以上信息解答下列问题:
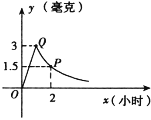
(1)求药物释放完毕后,y与x之间的函数关系式并写出自变量的取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进入教室,那么,从星期天下午5:00开始对某教室释放药物进行消毒,到星期一早上7:00时学生能否进入教室?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=.
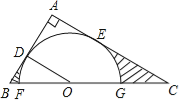
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某面粉厂从生产的袋装面粉中抽出样品20袋,检测每袋的质量是否符合标准,超过、不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值(单位:千克) | -0.3 | -0.2 | -0.1 | 0 | 0.1 | 0.2 |
袋数 | 3 | 2 | 4 | 6 | 3 | 2 |
(1)这批样品中最多的一袋比最少的一袋多多少千克?
(2)这20袋面粉的总质量比标准的质量多(或少)多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
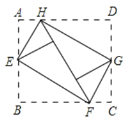
【题目】如图,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,则边AD的长是________ cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几何计算:
如图,已知∠AOB=40°,∠BOC=3∠AOB,OD平分∠AOC,求∠COD的度数.
解:因为∠BOC=3∠AOB,∠AOB=40°
所以∠BOC=__________°
所以∠AOC=__________ + _________
=__________° + __________°
=__________°
因为OD平分∠AOC
所以∠COD=![]() __________=__________°
__________=__________°

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,O,B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.
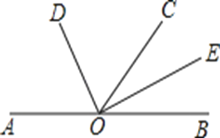
(1)若∠BOC=62°,求∠DOE的度数;
(2)若∠BOC=α,求∠DOE的度数;
(3)通过(1)(2)的计算,你能总结出什么结论,直接简写出来,不用说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校初一年级参加社会实践课,报名第一门课的有x人,第二门课的人数比第一门课的![]() 少20人,现在需要从报名第二门课的人中调出10人学习第一门课,那么用含x的式子解答下题.
少20人,现在需要从报名第二门课的人中调出10人学习第一门课,那么用含x的式子解答下题.
(1)报两门课的共有多少人?
(2)调动后,报名第一门课比报名第二门课多多少人?计算出代数式后,请选择一个你觉得合适的x值代入,并求出具体人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
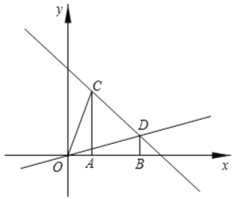
【题目】在平面直角坐标系中,过点C(1,3)、D(3,1)分别作x轴的垂线,垂足分别为A、B.
(1)求直线CD和直线OD的解析式;
(2)点M为直线OD上的一个动点,过M作x轴的垂线交直线CD于点N,是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;
(3)若△AOC沿CD方向平移(点C在线段CD上,且不与点D重合),在平移的过程中,设平移距离为![]() t,△AOC与△OBD重叠部分的面积记为s,试求s与t的函数关系式.
t,△AOC与△OBD重叠部分的面积记为s,试求s与t的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com