
【题目】为了预防流感,某学校在星期天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(小时)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据以上信息解答下列问题:
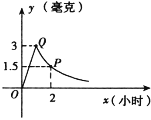
(1)求药物释放完毕后,y与x之间的函数关系式并写出自变量的取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进入教室,那么,从星期天下午5:00开始对某教室释放药物进行消毒,到星期一早上7:00时学生能否进入教室?
【答案】(1) ![]() , x>1(或 x≥1);早上 7:00 时学生能够进入教室.
, x>1(或 x≥1);早上 7:00 时学生能够进入教室.
【解析】
首先根据题意,药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,将数据代入用待定系数法可得反比例函数的关系式;进一步求解可得答案.
解:(1) 设药物释放完毕后 y 与 x 的函数关系式为
![]() 由题意,得
由题意,得![]()
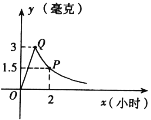
∴药物释放完毕后的函数关系式为![]()
在![]() 中,令 y=3,得 x=1.
中,令 y=3,得 x=1.
∴Q(1,3).
∴在![]() 中,自变量 x 的取值范围为 x >1(或 x≥1).
中,自变量 x 的取值范围为 x >1(或 x≥1).
(2) 解不等式![]() ,得 x>12.
,得 x>12.
∵从星期天下午 5:00 到星期一早上 7:00 时,共有 12-5+7=14(小时), 而 14>12,所以到星期一早上 7:00 时学生能够进入教室.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象经过点A(﹣1,a),过点A作AB⊥x轴,垂足为点B,△AOB的面积为
的图象经过点A(﹣1,a),过点A作AB⊥x轴,垂足为点B,△AOB的面积为![]() .
.
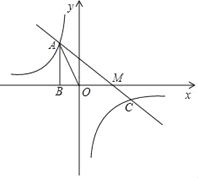
(1)求k的值;
(2)若一次函数y=mx+n图象经过点A和反比例函数图象上另一点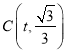 ,且与x轴交于M点,求AM的值;
,且与x轴交于M点,求AM的值;
(3)在(2)的条件下,如果以线段AM为一边作等边△AMN,顶点N在另一个反比例函数![]() 上,则k'= .
上,则k'= .
查看答案和解析>>
科目:初中数学 来源: 题型:
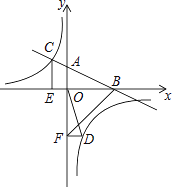
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数![]() 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F连接OD、BF,如果![]() ,求点D的坐标.
,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展旅游经济,我市某景区对门票采用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分的游客打b折售票.设某旅游团人数为x人,非节假日购票款为![]() (元),节假日购票款为
(元),节假日购票款为![]() (元).
(元).![]() ,
,![]() 与x之间的函数图象如图所示.
与x之间的函数图象如图所示.
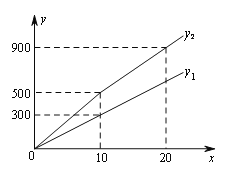
(1)观察图象可知:a= ;b= ;m= ;
(2)直接写出![]() ,
,![]() 与x之间的函数关系式;
与x之间的函数关系式;
(3)某旅行社导游王娜于5月1日带A团,5月20日(非节假日)带B团都到该景区旅游,共付门票款1900元,A,B两个团队合计50人,求A,B两个团队各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
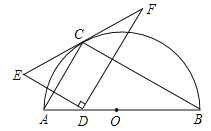
【题目】如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:
①CE=CF;
②线段EF的最小值为![]() ;
;
③当AD=2时,EF与半圆相切;
④若点F恰好落在B C上,则AD=![]() ;
;
⑤当点D从点A运动到点B时,线段EF扫过的面积是![]() .
.
其中正确结论的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,已知AD∥BC,AB=DC,AD=2,BC=4,延长BC到E,使CE=AD.
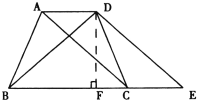
(1)写出图中所有与△DCE全等的三角形,并选择其中一对说明全等的理由;
(2)探究:当梯形ABCD的高DF等于多少时,对角线AC与BD互相垂直?请回答并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
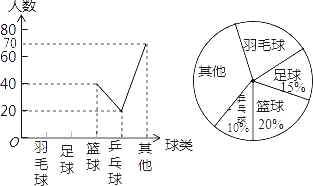
【题目】某中学在实施快乐大课间之前组织过“我最喜欢的球类”的调查活动,每个学生仅选择一项,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制成的不完整统计图.
(1)求出被调查的学生人数;
(2)把折线统计图补充完整;
(3)小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.如果确定小亮打第一场,其余三人用“手心、手背”的方法确定谁获胜谁打第一场若三人中有一人出的与其余两人不同则获胜;若三人出的都相同则平局.已知大刚出手心,请用树状图分析大刚获胜的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
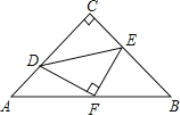
【题目】如图,已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD,FE分别交AC,BC于点D,E两点,当∠DFE在△ABC内绕顶点F旋转时(点D不与A,C重合),给出以下个结论:①CD=BE;②四边形CDFE不可能是正方形;③△DFE是等腰直角三角形;④S四边形CDFE=![]() S△ABC.上述结论中始终正确的有______.(填序号)
S△ABC.上述结论中始终正确的有______.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读下面材料:
点A、B在数轴上分别表示实数a、b, A、B两点之间的距离表示为AB,若a≥b,则 | a-b | = a-b;若a < b,则 | a-b | = b-a,当A、B两点中有一点在原点时, 不妨设点A在原,
如图甲, AB = OB =∣b∣=∣a b∣;当A、B两点都不在原点时,
![]()
① 如图乙,点A、B都在原点的右边,AB=OBOA=|b||a|=ba =|ab |;
![]()
②如图丙,点A、B都在原点的左边, AB = OB OA =|b||a|= b (a) = |ab|;
![]()
③如图丁,点A、B在原点的两边AB=OA+OB=|a|+|b|=a+(b) =|ab|.
![]()
综上所述,数轴上A、B两点之间的距离AB=∣ab∣.
(2)回答下列问题:
①数轴上表示1和3的两点之间的距离是______,数轴上表示1和3的两点之间的距离是______;
②数轴上表示x和1的两点分别是点A和B,则A、B之间的距离表示为______,如果AB=2,那么x =________ ;
③当代数式∣x +1∣+∣x 3∣取最小值时,相应的x的取值范围是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com