
【题目】如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:
①CE=CF;
②线段EF的最小值为![]() ;
;
③当AD=2时,EF与半圆相切;
④若点F恰好落在B C上,则AD=![]() ;
;
⑤当点D从点A运动到点B时,线段EF扫过的面积是![]() .
.
其中正确结论的序号是 .
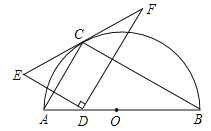
【答案】①③⑤.
【解析】试题分析:①连接CD,如图1所示,∵点E与点D关于AC对称,∴CE=CD,∴∠E=∠CDE,∵DF⊥DE,∴∠EDF=90°,∴∠E+∠F=90°,∠CDE+∠CDF=90°,∴∠F=∠CDF,∴CD=CF,∴CE=CD=CF,∴结论“CE=CF”正确;
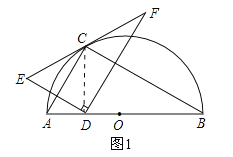
②当CD⊥AB时,如图2所示,∵AB是半圆的直径,∴∠ACB=90°,∵AB=8,∠CBA=30°,∴∠CAB=60°,AC=4,BC=![]() .∵CD⊥AB,∠CBA=30°,∴CD=
.∵CD⊥AB,∠CBA=30°,∴CD=![]() BC=
BC=![]() .根据“点到直线之间,垂线段最短”可得:点D在线段AB上运动时,CD的最小值为
.根据“点到直线之间,垂线段最短”可得:点D在线段AB上运动时,CD的最小值为![]() .∵CE=CD=CF,∴EF=2CD.∴线段EF的最小值为
.∵CE=CD=CF,∴EF=2CD.∴线段EF的最小值为![]() .∴结论“线段EF的最小值为
.∴结论“线段EF的最小值为![]() ”错误;
”错误;
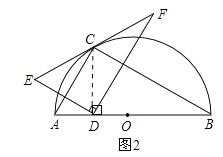
③当AD=2时,连接OC,如图3所示,∵OA=OC,∠CAB=60°,∴△OAC是等边三角形,∴CA=CO,∠ACO=60°,∵AO=4,AD=2,∴DO=2,∴AD=DO,∴∠ACD=∠OCD=30°,∵点E与点D关于AC对称,∴∠ECA=∠DCA,∴∠ECA=30°,∴∠ECO=90°,∴OC⊥EF,∵EF经过半径OC的外端,且OC⊥EF,∴EF与半圆相切,∴结论“EF与半圆相切”正确;
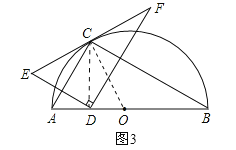
④当点F恰好落在![]() 上时,连接FB、AF,如图4所示,∵点E与点D关于AC对称,∴ED⊥AC,∴∠AGD=90°,∴∠AGD=∠ACB,∴ED∥BC,∴△FHC∽△FDE,∴FH:FD=FC:FE,∵FC=
上时,连接FB、AF,如图4所示,∵点E与点D关于AC对称,∴ED⊥AC,∴∠AGD=90°,∴∠AGD=∠ACB,∴ED∥BC,∴△FHC∽△FDE,∴FH:FD=FC:FE,∵FC=![]() EF,∴FH=
EF,∴FH=![]() FD,∴FH=DH,∵DE∥BC,∴∠FHC=∠FDE=90°,∴BF=BD,∴∠FBH=∠DBH=30°,∴∠FBD=60°,∵AB是半圆的直径,∴∠AFB=90°,∴∠FAB=30°,∴FB=
FD,∴FH=DH,∵DE∥BC,∴∠FHC=∠FDE=90°,∴BF=BD,∴∠FBH=∠DBH=30°,∴∠FBD=60°,∵AB是半圆的直径,∴∠AFB=90°,∴∠FAB=30°,∴FB=![]() AB=4,∴DB=4,∴AD=AB﹣DB=4,∴结论“AD=
AB=4,∴DB=4,∴AD=AB﹣DB=4,∴结论“AD=![]() ”错误;
”错误;
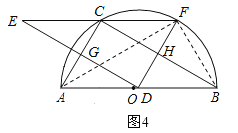
⑤∵点D与点E关于AC对称,点D与点F关于BC对称,∴当点D从点A运动到点B时,点E的运动路径AM与AB关于AC对称,点F的运动路径NB与AB关于BC对称,∴EF扫过的图形就是图5中阴影部分,∴S阴影=2S△ABC=2×![]() ACBC=ACBC=4×
ACBC=ACBC=4×![]() =
=![]() ,∴EF扫过的面积为
,∴EF扫过的面积为![]() ,∴结论“EF扫过的面积为
,∴结论“EF扫过的面积为![]() ”正确.
”正确.
故答案为:①③⑤.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】一列货车从北京开往乌鲁木齐,以58km/h的平均速度行驶需要65h.为了实施西部大开发,京乌线决定全线提速.
(1)如果提速后平均速度为vkm/h,全程运营时间为t小时,试写出t与v之间的函数表达式;
(2)如果提速后平均速度为78km/h,求提速后全程运营时间;
(3)如果全程运营的时间控制在40h内,那么提速后,平均速度至少应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)某商场统计了今年1~5月A,B两种品牌冰箱的销售情况,并将获得的数据绘制成折线统计图.
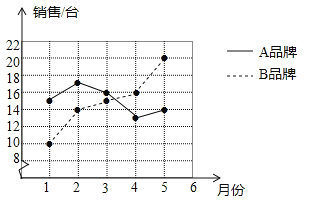
(1)分别求该商场这段时间内A,B两种品牌冰箱月销售量的中位数和方差;
(2)根据计算结果,比较该商场1~5月这两种品牌冰箱月销售量的稳定性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学改革学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.小华与小明同学就“你最喜欢哪种学习方式”随机调查了他们周围的一些同学,根据收集到的数据绘制了以下两个不完整的统计图(如图).


请根据上面两个不完整的统计图回答以下4个问题:
(1)这次抽样调查中,共调查了_____名学生.
(2)补全条形统计图中的缺项.
(3)在扇形统计图中,选择教师传授的占_____%,选择小组合作学习的占_____%.
(4)根据调查结果,估算该校1800名学生中大约有_____人选择小组合作学习模式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防流感,某学校在星期天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(小时)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据以上信息解答下列问题:
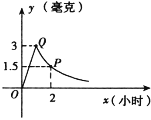
(1)求药物释放完毕后,y与x之间的函数关系式并写出自变量的取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进入教室,那么,从星期天下午5:00开始对某教室释放药物进行消毒,到星期一早上7:00时学生能否进入教室?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:Rt△A′BC′≌Rt△ABC,∠A′C′B=∠ACB=90°,∠A′BC′=∠ABC=60°,Rt△A′BC′可绕点B旋转,设旋转过程中直线CC′和AA′相交于点D.
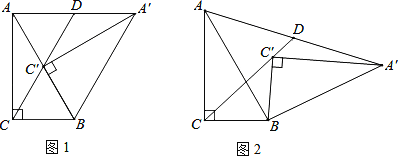
(1)如图1所示,当点C′在AB边上时,判断线段AD和线段A′D之间的数量关系,并证明你的结论;
(2)将Rt△A′BC′由图1的位置旋转到图2的位置时,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)将Rt△A′BC′由图1的位置按顺时针方向旋转α角(0°≤α≤120°),当A、C′、A′三点在一条直线上时,请直接写出旋转角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,则边AD的长是________ cm.
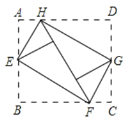
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com