
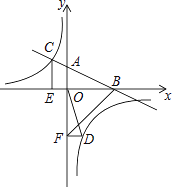
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数![]() 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F连接OD、BF,如果![]() ,求点D的坐标.
,求点D的坐标.
【答案】(1)![]() ;(2)点D的坐标为(
;(2)点D的坐标为(![]() ,﹣4).
,﹣4).
【解析】试题分析:(1)由边的关系可得出BE=6,通过解直角三角形可得出CE=3,结合函数图象即可得出点C的坐标,再根据点C的坐标利用反比例函数图象上点的坐标特征,即可求出反比例函数系数k,由此即可得出结论;
(2)由点D在反比例函数在第四象限的图象上,设出点D的坐标为(n,﹣![]() )(n>0).通过解直角三角形求出线段OA的长度,再利用三角形的面积公式利用含n的代数式表示出S△BAF,根据点D在反比例函数图形上利用反比例函数系数k的几何意义即可得出S△DFO的值,结合题意给出的两三角形的面积间的关系即可得出关于n的分式方程,解方程,即可得出n值,从而得出点D的坐标.
)(n>0).通过解直角三角形求出线段OA的长度,再利用三角形的面积公式利用含n的代数式表示出S△BAF,根据点D在反比例函数图形上利用反比例函数系数k的几何意义即可得出S△DFO的值,结合题意给出的两三角形的面积间的关系即可得出关于n的分式方程,解方程,即可得出n值,从而得出点D的坐标.
试题解析:解:(1)∵OB=4,OE=2,∴BE=OB+OE=6.∵CE⊥x轴,∴∠CEB=90°.
在Rt△BEC中,∠CEB=90°,BE=6,tan∠ABO=![]() ,∴CE=BEtan∠ABO=6×
,∴CE=BEtan∠ABO=6×![]() =3,结合函数图象可知点C的坐标为(﹣2,3).
=3,结合函数图象可知点C的坐标为(﹣2,3).
∵点C在反比例函数y=![]() 的图象上,∴k=﹣2×3=﹣6,∴反比例函数的解析式为y=﹣
的图象上,∴k=﹣2×3=﹣6,∴反比例函数的解析式为y=﹣![]() .
.
(2)∵点D在反比例函数y=﹣![]() 第四象限的图象上,∴设点D的坐标为(n,﹣
第四象限的图象上,∴设点D的坐标为(n,﹣![]() )(n>0).
)(n>0).
在Rt△AOB中,∠AOB=90°,OB=4,tan∠ABO=![]() ,∴OA=OBtan∠ABO=4×
,∴OA=OBtan∠ABO=4×![]() =2.
=2.
∵S△BAF=![]() AFOB=
AFOB=![]() (OA+OF)OB=
(OA+OF)OB=![]() (2+
(2+![]() )×4=4+
)×4=4+![]() .
.
∵点D在反比例函数y=﹣![]() 第四象限的图象上,∴S△DFO=
第四象限的图象上,∴S△DFO=![]() ×|﹣6|=3.
×|﹣6|=3.
∵S△BAF=4S△DFO,∴4+![]() =4×3,解得:n=
=4×3,解得:n=![]() ,经验证,n=
,经验证,n=![]() 是分式方程4+
是分式方程4+![]() =4×3的解,∴点D的坐标为(
=4×3的解,∴点D的坐标为(![]() ,﹣4).
,﹣4).


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,sinA=![]() ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
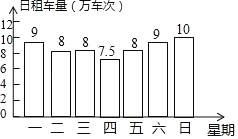
【题目】摩拜公司为了调查在某市投放的共享单车使用情况,对4月份第一个星期中每天摩拜单车使用情况进行统计,结果如图所示.
(1)求这一个星期每天单车使用情况的众数、中位数和平均数;
(2)用(1)中的结果估计4月份一共有多少万车次?
(3)摩拜公司在该市共享单车项目中共投入9600万元,估计本年度共租车3200万车次,若每车次平均收入租车费0.75元,请估计本年度全年租车费收入占总投入的百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
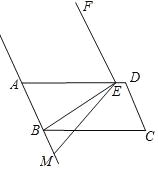
【题目】如图,四边形ABCD为平行四边形,过点B作BE⊥AB交AD于点E,将线段BE绕点E顺时针旋转90°到EF的位置,点M(点M不与点B重合)在直线AB上,连结EM.
(1)当点M在线段AB的延长线上时,将线段EM绕点E顺时针旋转90°到EN1的位置,连结FN1,在图中画出图形,求证:FN1⊥AB;
(2)当点M在线段BA的延长线上时,将线段EM绕点E顺时针旋转90°到EN2的位置,连结FN2,在图中画出图形,点N2在直线FN1上吗?请说明理由;
(3)若AB=3,AD=6,DE=1,设BM=x,在(1)、(2)的条件下,试用含x的代数式表示△FMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
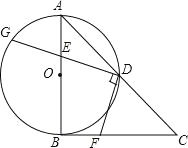
(1)求证:AE=BF;
(2)连接GB,EF,求证:GB∥EF;
(3)若AE=1,EB=2,求DG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)某商场统计了今年1~5月A,B两种品牌冰箱的销售情况,并将获得的数据绘制成折线统计图.
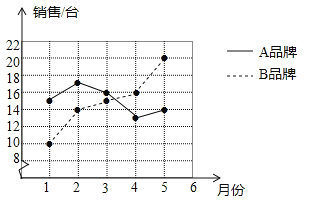
(1)分别求该商场这段时间内A,B两种品牌冰箱月销售量的中位数和方差;
(2)根据计算结果,比较该商场1~5月这两种品牌冰箱月销售量的稳定性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防流感,某学校在星期天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(小时)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据以上信息解答下列问题:
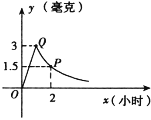
(1)求药物释放完毕后,y与x之间的函数关系式并写出自变量的取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进入教室,那么,从星期天下午5:00开始对某教室释放药物进行消毒,到星期一早上7:00时学生能否进入教室?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=.
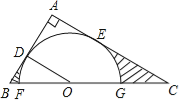
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com