
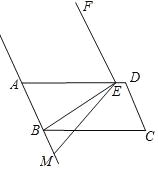
【题目】如图,四边形ABCD为平行四边形,过点B作BE⊥AB交AD于点E,将线段BE绕点E顺时针旋转90°到EF的位置,点M(点M不与点B重合)在直线AB上,连结EM.
(1)当点M在线段AB的延长线上时,将线段EM绕点E顺时针旋转90°到EN1的位置,连结FN1,在图中画出图形,求证:FN1⊥AB;
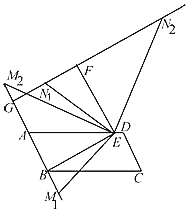
(2)当点M在线段BA的延长线上时,将线段EM绕点E顺时针旋转90°到EN2的位置,连结FN2,在图中画出图形,点N2在直线FN1上吗?请说明理由;
(3)若AB=3,AD=6,DE=1,设BM=x,在(1)、(2)的条件下,试用含x的代数式表示△FMN的面积.
【答案】(1)证明见解析;(2)点N2在直线FN1上;(3)S1=2x+![]() x2(x>0);S2=2x-
x2(x>0);S2=2x-![]() x2(3<x<4);S3=
x2(3<x<4);S3=![]() x2-2x(x>4).
x2-2x(x>4).
【解析】
(1)首先证明△EBM1≌△EFN1,再证明四边形BEFG为矩形,因此证明FN1⊥AB.
(2)首先证明△EBM2≌△EFN2,即可得∠EFN2=90°,再根据∠EFN1+∠EFN2=180°,即可得点N2在直线FN1上.
(3)根据(1)的四边形BEFG为正方形,即可计算AE,再利用在Rt△ABE中,结合勾股定理计算BE,进而分情况讨论.
(1)证明:如图,∵∠BEF=∠M1EN1=90°,
∴∠BEM1=∠FEN1,
∵DB=DF,EM1=EN1
∴△EBM1≌△EFN1,
∴∠EFN1=∠EBM1,
∵EB⊥AB,
∴∠EBM1=90°
∴∠EFN1=90°,
∴四边形BEFG为矩形,
∴∠FGB=90°
即FN1⊥AB.
(2)如图,跟(1)同理可证△EBM2≌△EFN2,则∠EFN2=90°,
由于∠EFN1+∠EFN2=180°,所以点N2在直线FN1上.
(3)由(1)可知四边形BEFG为正方形,
∵AD=6,DE=1,
∴AE=5,
在Rt△ABE中,BE=![]() =4,
=4,
当点M1在线段AB的延长线上时,S1=![]() x(4+x)=2x+
x(4+x)=2x+![]() x2,此时x>0;
x2,此时x>0;
当点M2在线段BA的延长线上时,
①当3<x<4时,S2=![]() x(4-x)=2x-
x(4-x)=2x-![]() x2.
x2.
②当x>4时,S3=![]() x(x-4)=
x(x-4)=![]() x2-2x.
x2-2x.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】市百货商场元月一日搞促销活动,购物不超过![]() 元不给优惠;超过
元不给优惠;超过![]() 元,而不足
元,而不足![]() 元按总价优惠
元按总价优惠![]() ;超过
;超过![]() 元的其中
元的其中![]() 元按
元按![]() 折优惠,超过部分按
折优惠,超过部分按![]() 折优惠.某人两次购物分别用了
折优惠.某人两次购物分别用了![]() 元和
元和![]() 元.问:
元.问:
(1)此人两次购物其物品如果不打折,两次购物价值_____元和_____元.
(2)在此活动中,通过打折他节省了多少钱?
(3)若此人将两次购物的钱合起来购相同的商品与两次分别购买是更节省还是亏损?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象经过点A(﹣1,a),过点A作AB⊥x轴,垂足为点B,△AOB的面积为
的图象经过点A(﹣1,a),过点A作AB⊥x轴,垂足为点B,△AOB的面积为![]() .
.
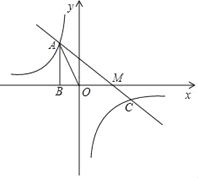
(1)求k的值;
(2)若一次函数y=mx+n图象经过点A和反比例函数图象上另一点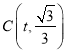 ,且与x轴交于M点,求AM的值;
,且与x轴交于M点,求AM的值;
(3)在(2)的条件下,如果以线段AM为一边作等边△AMN,顶点N在另一个反比例函数![]() 上,则k'= .
上,则k'= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分,而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了,有一种用“因式分解”法产生的密码、方便记忆,其原理是:将一个多项式分解因式,如多项式:![]() 因式分解的结果为
因式分解的结果为![]() ,当
,当![]() 时,
时,![]() 此时可以得到数字密码171920.
此时可以得到数字密码171920.
(1)根据上述方法,当![]() 时,对于多项式
时,对于多项式![]() 分解因式后可以形成哪些数字密码?(写出三个)
分解因式后可以形成哪些数字密码?(写出三个)
(2)若一个直角三角形的周长是24,斜边长为10,其中两条直角边分别为x、y,求出一个由多项式![]() 分解因式后得到的密码(只需一个即可);
分解因式后得到的密码(只需一个即可);
(3)若多项式![]() 因式分解后,利用本题的方法,当
因式分解后,利用本题的方法,当![]() 时可以得到其中一个密码为242834,求m、n的值.
时可以得到其中一个密码为242834,求m、n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上原点左边有一点A,点A对应着数a,有如下说法:
①﹣a表示的数一定是一个正数.
②若|a|=9时,则a=﹣9.
③在﹣a,![]() ,a2,a3中,最大的数值是a2.
,a2,a3中,最大的数值是a2.
④式子|a+![]() |的最小值为2.
|的最小值为2.
其中正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 “已知:正比例函数y1=kx(k>0)与反比例函数y2=![]() (m>0)图象相交于A、B两点,其横坐标分别是1和﹣1,求不等式kx>
(m>0)图象相交于A、B两点,其横坐标分别是1和﹣1,求不等式kx>![]() 的解集.”对于这道题,某同学是这样解答的:“由图象可知:当x>1或﹣1<x<0时,y1>y2,所以不等式kx>
的解集.”对于这道题,某同学是这样解答的:“由图象可知:当x>1或﹣1<x<0时,y1>y2,所以不等式kx>![]() 的解集是x>1或﹣1<x<0”.他这种解决问题的思路体现的数学思想方法是( )
的解集是x>1或﹣1<x<0”.他这种解决问题的思路体现的数学思想方法是( )
A.数形结合 B.转化 C.类比 D.分类讨论
查看答案和解析>>
科目:初中数学 来源: 题型:
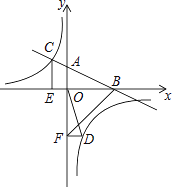
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数![]() 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F连接OD、BF,如果![]() ,求点D的坐标.
,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展旅游经济,我市某景区对门票采用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分的游客打b折售票.设某旅游团人数为x人,非节假日购票款为![]() (元),节假日购票款为
(元),节假日购票款为![]() (元).
(元).![]() ,
,![]() 与x之间的函数图象如图所示.
与x之间的函数图象如图所示.
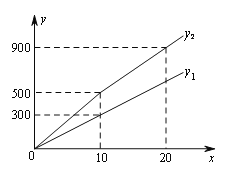
(1)观察图象可知:a= ;b= ;m= ;
(2)直接写出![]() ,
,![]() 与x之间的函数关系式;
与x之间的函数关系式;
(3)某旅行社导游王娜于5月1日带A团,5月20日(非节假日)带B团都到该景区旅游,共付门票款1900元,A,B两个团队合计50人,求A,B两个团队各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
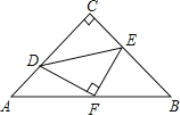
【题目】如图,已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD,FE分别交AC,BC于点D,E两点,当∠DFE在△ABC内绕顶点F旋转时(点D不与A,C重合),给出以下个结论:①CD=BE;②四边形CDFE不可能是正方形;③△DFE是等腰直角三角形;④S四边形CDFE=![]() S△ABC.上述结论中始终正确的有______.(填序号)
S△ABC.上述结论中始终正确的有______.(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com