
【题目】如图,已知反比例函数![]() 的图象经过点A(﹣1,a),过点A作AB⊥x轴,垂足为点B,△AOB的面积为
的图象经过点A(﹣1,a),过点A作AB⊥x轴,垂足为点B,△AOB的面积为![]() .
.
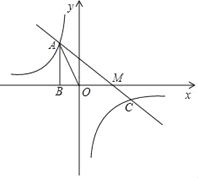
(1)求k的值;
(2)若一次函数y=mx+n图象经过点A和反比例函数图象上另一点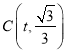 ,且与x轴交于M点,求AM的值;
,且与x轴交于M点,求AM的值;
(3)在(2)的条件下,如果以线段AM为一边作等边△AMN,顶点N在另一个反比例函数![]() 上,则k'= .
上,则k'= .
【答案】(1)![]() ;(2)
;(2)![]() ;(3):4
;(3):4![]() 或
或![]() .
.
【解析】
(1)根据点A的坐标以及三角形的面积公式即可求出a值,再根据反比例函数图象上点的坐标特征即可求出k的值;
(2)根据反比例函数解析式可求出点C的坐标,由点A、C的坐标利用待定系数法即可求出直线AM的解析式,令直线AM的解析式中y=0求出x值,即可得出点M的坐标,再利用勾股定理即可求出线段AM的长度;
(3)设点N的坐标为(m,n),由等边三角形的性质结合三角函数找出关于m、n的关系来求得点N.
解:(1)∵S△AOB=![]() OBAB=
OBAB=![]() ,
,
∴![]() ×1×a=
×1×a=![]() ,
,
∴a=![]() .
.
∴点A(﹣1,![]() ).
).
∵反比例函数y=![]() 的图象经过点A (﹣1,
的图象经过点A (﹣1,![]() ),
),
∴k=﹣![]() .
.
(2)∵C (t,![]() )在反比例函数y=
)在反比例函数y=![]() 的图象上,
的图象上,
∴![]() t=﹣
t=﹣![]() ,解得:t=3,
,解得:t=3,
∴C(3,![]() ).
).
将A(﹣1,![]() )、C(3,
)、C(3,![]() )代入y=mx+n中,
)代入y=mx+n中,
得:![]() ,解得:
,解得: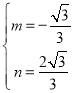 ,
,
∴直线AM的解析式为y=![]() x+
x+![]() .
.
令y=![]() x+
x+![]() 中y=0,则x=2,
中y=0,则x=2,
∴M(2,0).
在Rt△ABM中,AB=![]() ,BM=2﹣(﹣1)=3,
,BM=2﹣(﹣1)=3,
∴AM=![]() =2
=2![]() .
.
(3)设点N的坐标为(m,n),
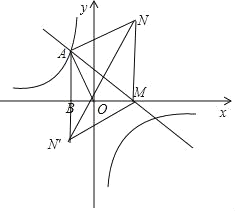
∵△AMN为等边三角形,且AM=2![]() .
.
∴∠AMN=60°,
∵tan∠AMB=![]() =
=![]() ,
,
∴∠AMB=30°,
∴∠NMB=90°,
∴N(2,2![]() ),
),
同法可得:当△AMN′是等边三角形时,可得N′(﹣1,﹣![]() ),
),
∵顶点N在另一个反比例函数y=![]() 上,
上,
∴k′=4![]() 或
或![]()
故答案为:4![]() 或
或![]() .
.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】将下列各数填在相应的集合里。
-3.8, -20%, 4.3, -∣-![]() ∣,
∣, ![]() , 0, -(-
, 0, -(-![]() ),
), ![]()
整数集合:{ … };
分数集合:{ … };
正数集合:{ … };
负数集合:{ … }.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,sinA=![]() ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】砀山酥梨是一种驰名中外的特色水果,它是梨的一种,因为出产于砀山县而得名。现有20筐砀山酥梨,以每筐25千克的质量为标准,超过或不足的千克数分别用正、负数来表示,记录如下:

(1)这20筐砀山酥梨中,最重的一筐比最轻的一筐重多少千克?
(2)与标准质量比较,这20筐砀山酥梨总计超过或不足多少千克?
(3)若砀山酥梨每千克售价4元,则这20筐砀山酥梨可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列货车从北京开往乌鲁木齐,以58km/h的平均速度行驶需要65h.为了实施西部大开发,京乌线决定全线提速.
(1)如果提速后平均速度为vkm/h,全程运营时间为t小时,试写出t与v之间的函数表达式;
(2)如果提速后平均速度为78km/h,求提速后全程运营时间;
(3)如果全程运营的时间控制在40h内,那么提速后,平均速度至少应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,已知抛物线y=ax2+bx﹣5与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C.
(1)求抛物线的函数表达式;
(2)如图2,CE∥x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别相交于点F,G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标;
(3)若点K为抛物线的顶点,点M(4,m)是该抛物线上的一点,在x轴,y轴上分别找点P,Q,使四边形PQKM的周长最小,求出点P,Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
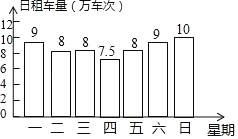
【题目】摩拜公司为了调查在某市投放的共享单车使用情况,对4月份第一个星期中每天摩拜单车使用情况进行统计,结果如图所示.
(1)求这一个星期每天单车使用情况的众数、中位数和平均数;
(2)用(1)中的结果估计4月份一共有多少万车次?
(3)摩拜公司在该市共享单车项目中共投入9600万元,估计本年度共租车3200万车次,若每车次平均收入租车费0.75元,请估计本年度全年租车费收入占总投入的百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
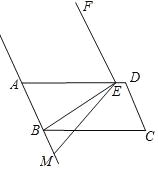
【题目】如图,四边形ABCD为平行四边形,过点B作BE⊥AB交AD于点E,将线段BE绕点E顺时针旋转90°到EF的位置,点M(点M不与点B重合)在直线AB上,连结EM.
(1)当点M在线段AB的延长线上时,将线段EM绕点E顺时针旋转90°到EN1的位置,连结FN1,在图中画出图形,求证:FN1⊥AB;
(2)当点M在线段BA的延长线上时,将线段EM绕点E顺时针旋转90°到EN2的位置,连结FN2,在图中画出图形,点N2在直线FN1上吗?请说明理由;
(3)若AB=3,AD=6,DE=1,设BM=x,在(1)、(2)的条件下,试用含x的代数式表示△FMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防流感,某学校在星期天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(小时)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据以上信息解答下列问题:
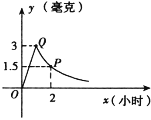
(1)求药物释放完毕后,y与x之间的函数关系式并写出自变量的取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进入教室,那么,从星期天下午5:00开始对某教室释放药物进行消毒,到星期一早上7:00时学生能否进入教室?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com