
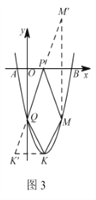
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���֪������y=ax2+bx��5��x�ύ��A����1��0����B��5��0�����㣬��y�ύ�ڵ�C��
��1���������ߵĺ�������ʽ��
��2����ͼ2��CE��x�����������ཻ�ڵ�E����H��ֱ��CE�·��������ϵĶ��㣬����H����y��ƽ�е�ֱ����BC��CE�ֱ��ཻ�ڵ�F��G����̽������H�˶����δ�ʱ���ı���CHEF�����������H�����ꣻ
��3������KΪ�����ߵĶ��㣬��M��4��m���Ǹ��������ϵ�һ�㣬��x�ᣬy���Ϸֱ��ҵ�P��Q��ʹ�ı���PQKM���ܳ���С�������P��Q�����꣮

���𰸡���1��y=x2��4x��5��2����![]() ����
����![]() ������3��P��
������3��P��![]() ��0����Q��0����
��0����Q��0����![]() ��
��
�����������������
��1���ô���ϵ�����������ߵĽ���ʽ����2����H(t��t2-4t-5)���ú�t�Ĵ���ʽ��ʾFH�ij������CE�ij����öԽ����ഹֱ���ı��ε�������ڶԽ�����һ�룬���ı���CHEF�������ʾΪ����t�Ķ��κ������ö��κ�����������⣻��3������M��K����x�ᣬy��ԳƵ�M�䣬K��������M��K�䣬�ֱ�x����y���ڵ�P��Q�����M��K���Ľ���ʽ�����ɵõ���P��Q������.
������1����A(-1��0)��B(5��0)����y=ax2+bx-5��
![]() �����
�����![]()
����κ����ı���ʽΪy=x2-4x-5
��2����ͼ2����H(t��t2-4t-5)��
��CE||x�ᣬ��-5=x2-4x-5����ã�x1=0��x2=4��
��E(4��-5)����CE=4��
��B(5��0)��C(0��-5)��
![]() ��
��![]() ��
��
��ֱ��BC�Ľ���ʽΪy2=x-5����F(t��t-5)��
��CE||x�ᣬHF||y�ᣬ��CE��HF��
���ı���CHEF�����=![]() )2+
)2+![]() ��
��
��H(![]() .
.
��3����ͼ3��
�ߵ�KΪ���㣬��K(2��-9)��
���K����y��ĶԳƵ�K��������Ϊ(-2��-9)��
��M(4��m)����M(4��-5)��
���M����x��ĶԳƵ�M��������Ϊ(4��5)��
��ֱ��K��M���Ľ���ʽΪy3=a3x+b3��
![]() ����
����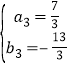
��ֱ��BC�Ľ���ʽΪy3=![]() ��
��
��P��Q������ֱ�ΪP(![]() ��0)��Q(0��-
��0)��Q(0��-![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��Ϊ���꽫Ҫ�μ��п��ĺ���С��������һ������ͼ����������Ʒ�У������ϸ���һ�֣�������������Ԥף�п��ɹ�����������Ԥ���Ķ��������������������Ķ�������������������ƽ��չ��ͼ�����ǣ� ��
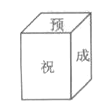
A.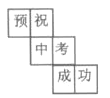 B.
B.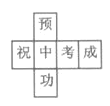 C.
C.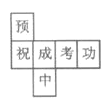 D.
D.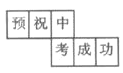
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
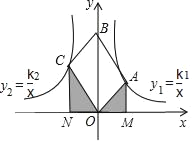
����Ŀ����ͼ���ı���OABC��ƽ���ı��Σ��Խ���OB��y���������ϣ�λ�ڵ�һ���ĵ�A�͵ڶ����ĵ�C�ֱ���˫����y1��![]() ��y2��
��y2��![]() ��һ֧�ϣ��ֱ����A��C��x��Ĵ��ߣ�����ֱ�ΪM��N���������µĽ��ۣ���
��һ֧�ϣ��ֱ����A��C��x��Ĵ��ߣ�����ֱ�ΪM��N���������µĽ��ۣ���![]() ����Ӱ���������
����Ӱ���������![]() ��k1��k2��������AOC��90��ʱ��|k1|��|k2|�������ı���OABC�����Σ�����˫���ȹ���x��Գƣ�Ҳ����y��Գƣ�������ȷ�Ľ�����_____��
��k1��k2��������AOC��90��ʱ��|k1|��|k2|�������ı���OABC�����Σ�����˫���ȹ���x��Գƣ�Ҳ����y��Գƣ�������ȷ�Ľ�����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ϵ�A��ʾ��20����C��ʾ��30�����ǰ�����������֮��ľ����ñ�ʾ����Ĵ�д��ĸһ����.
���磬��A���B֮��ľ������AB����B���C֮��ľ������BC��
![]()
(1)��A���C֮��ľ������AC����AC�ij�Ϊ________������������һ��D����CD=AD����D���ʾ����Ϊ___________��
(2)����B����1��Ӧ�ĵ㿪ʼ�����˶����ٶ�Ϊÿ��1����λ���ȣ�ͬʱ��A��C���������˶�����A��C���ٶȷֱ�Ϊÿ��2����λ���ȣ�ÿ��3����λ���ȣ��˶�ʱ��Ϊt��.
������A�����˶�����C�����˶���AB=BC����t��ֵ��
������A�����˶�����C�����˶���2ABm��BC��ֵ����ʱ��t�ı仯���ı䣬��2ABm��BC��ֵΪ_____________(ֱ��д����).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����������![]() ��ͼ����A����1��a��������A��AB��x�ᣬ����Ϊ��B����AOB�����Ϊ
��ͼ����A����1��a��������A��AB��x�ᣬ����Ϊ��B����AOB�����Ϊ![]() ��
��
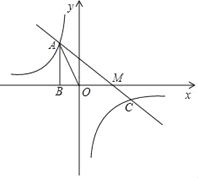
��1����k��ֵ��
��2����һ�κ���y��mx+nͼ����A�ͷ���������ͼ������һ��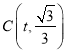 ������x�ύ��M�㣬��AM��ֵ��
������x�ύ��M�㣬��AM��ֵ��
��3���ڣ�2���������£�������߶�AMΪһ�����ȱߡ�AMN������N����һ������������![]() �ϣ���k'���� ����
�ϣ���k'���� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���MΪBC����һ�㣬BM��4MC����MΪֱ�Ƕ���������ֱ��������MEF����E�ڶԽ���BD�ϣ���F����������EF��BC�ڵ�N����CF����BE��2��S��CMF��3����MN��_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ֽ���������+����ʱ��,���������ǵ������Ѿ���������,�ܲ��ɷ�,��������123456�������յȼ����������ױ��ƽ�,������ü�������һ�������������ͺ��б�Ҫ��,��һ��������ʽ�ֽ��������������롢�������,��ԭ����:��һ������ʽ�ֽ���ʽ,�����ʽ:![]() ��ʽ�ֽ�Ľ��Ϊ
��ʽ�ֽ�Ľ��Ϊ![]() ,��
,��![]() ʱ,
ʱ,![]() ��ʱ���Եõ���������171920.
��ʱ���Եõ���������171920.
(1)������������,��![]() ʱ,���ڶ���ʽ
ʱ,���ڶ���ʽ![]() �ֽ���ʽ������γ���Щ��������?(д������)
�ֽ���ʽ������γ���Щ��������?(д������)
(2)��һ��ֱ�������ε��ܳ���24,б�߳�Ϊ10,��������ֱ�DZ߷ֱ�Ϊx��y,���һ���ɶ���ʽ![]() �ֽ���ʽ��õ�������(ֻ��һ������);
�ֽ���ʽ��õ�������(ֻ��һ������);
(3)������ʽ![]() ��ʽ�ֽ��,���ñ���ķ���,��
��ʽ�ֽ��,���ñ���ķ���,��![]() ʱ���Եõ�����һ������Ϊ242834,��m��n��ֵ.
ʱ���Եõ�����һ������Ϊ242834,��m��n��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ����֪������������y1=kx��k��0���뷴��������y2=![]() ��m��0��ͼ���ཻ��A��B���㣬�������ֱ���1�ͩ�1����ʽkx��
��m��0��ͼ���ཻ��A��B���㣬�������ֱ���1�ͩ�1����ʽkx��![]() �Ľ⼯������������⣬ijͬѧ���������ģ�����ͼ���֪����x��1��1��x��0ʱ��y1��y2�����Բ���ʽkx��
�Ľ⼯������������⣬ijͬѧ���������ģ�����ͼ���֪����x��1��1��x��0ʱ��y1��y2�����Բ���ʽkx��![]() �Ľ⼯��x��1��1��x��0���������ֽ�������˼·���ֵ���ѧ˼�뷽���ǣ� ��
�Ľ⼯��x��1��1��x��0���������ֽ�������˼·���ֵ���ѧ˼�뷽���ǣ� ��
A�����ν�� B��ת�� C����� D����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���֪AD��BC��AB��DC��AD��2��BC��4���ӳ�BC��E��ʹCE��AD��
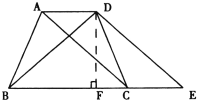
(1)д��ͼ���������DCEȫ�ȵ������Σ���ѡ������һ��˵��ȫ�ȵ����ɣ�
(2)̽����������ABCD�ĸ�DF���ڶ���ʱ���Խ���AC��BD���ഹֱ����ش�˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com