
����Ŀ����ͼ���������ϵ�A��ʾ��20����C��ʾ��30�����ǰ�����������֮��ľ����ñ�ʾ����Ĵ�д��ĸһ����.
���磬��A���B֮��ľ������AB����B���C֮��ľ������BC��
![]()
(1)��A���C֮��ľ������AC����AC�ij�Ϊ________������������һ��D����CD=AD����D���ʾ����Ϊ___________��
(2)����B����1��Ӧ�ĵ㿪ʼ�����˶����ٶ�Ϊÿ��1����λ���ȣ�ͬʱ��A��C���������˶�����A��C���ٶȷֱ�Ϊÿ��2����λ���ȣ�ÿ��3����λ���ȣ��˶�ʱ��Ϊt��.
������A�����˶�����C�����˶���AB=BC����t��ֵ��
������A�����˶�����C�����˶���2ABm��BC��ֵ����ʱ��t�ı仯���ı䣬��2ABm��BC��ֵΪ_____________(ֱ��д����).
���𰸡���1��50��5�� ��2����t=10��![]() ����-45��
����-45��
��������
��1���������ϱ�ʾ��������ɵ��߶γ������ұߵ�����ʾ������ȥ��ߵ�����ʾ�������ɣ�
��2�������������ʾ������֮��ľ��룬���ݾ���ֵ��������þ���ֵ���д������������������˶�������֪�˶��ķ�����ٶ�֮�Ϳ�������ԭ�����ڵ�����������ƶ��ͼ��������ƶ��ľ��룬��������ƶ����ͼ�ȥ�����ƶ��ľ��룮
�⣺��1����A��ʾ����Ϊ-20��C��ʾ����Ϊ30��
��AC=30-��-20��=50��
��CD=AD
���DΪAC���е�
��D����ʾ����Ϊ![]()
![]() =5��
=5��
�ʴ�Ϊ50��5
��2���ٸ������⣬A����ʾ����Ϊ-20+2t��C����ʾ����Ϊ30-3t��B����ʾ����Ϊ1+t��
AB=|-20+2t-��1+t��|=|-21+t|��
BC=|30-3t-��1+t��|=|29-4t|��
��AB=BC
��|-21+t|=|29-4t|��
-21+t=29-4t��
���t=10��
-21+t=4t-29
���t=![]() ��
��
�൱AB=BCʱ��t=10��![]() ��
��
�ڸ������⣬A����ʾ����Ϊ-20-2t��B����ʾ����Ϊ1+t��C����ʾ����Ϊ30+3t��
AB=1+t-��-20-2t��=21+3t��
BC=30+3t-��1+t��=29+2t��
��2AB-m��BC=2��21+3t��-m����29+2t��=42+6t-29m-2mt��
��2AB-m��BC��ֵ����ʱ��t�ı仯���ı䣬
��6t-2mt=0��
��m=3��
��42+6t-29m-2mt=-45��
��2AB-m��BC=-45��
�ʴ�Ϊ-45��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꼶��1���չ��Ϊ��һ�ܵġ����ϰ��ס������������ѧ���������ʱ�������������ڻ�еı���.��ʦ������ȫ��50��ѧ������λ���������ʱ�䣬����ͳ�Ƶ�ʱ�䣨��λ��Сʱ���ֳ�5�飺A��0.5��x��1��B��1��x��1.5��C��1.5��x��2��D��2��x��2.5��E��2.5��x��3��������������������ͳ��ͼ����ͼ��.
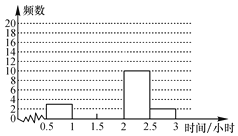
�����ͼ���ṩ����Ϣ������������⣺
��1����λ��ѧ��������ʱ�����λ�����ڵ�����____________��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3���ð��С��ͬѧ��һ��������2Сʱ������Ϊ�Լ��������ʱ��Ȱ���һ�����ϵ�ͬѧ�࣬����ΪС�����жϷ���ʵ���������ʵ���ͳ��֪ʶ˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���kx2+2x��1=0��ʵ������
��1����k��ȡֵ��Χ��
��2����k=2ʱ�������䷽����˷��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y��![]() x+b�ֱ�x�ᡢy���ڵ�A��C����P��ֱ��AC��˫����y��
x+b�ֱ�x�ᡢy���ڵ�A��C����P��ֱ��AC��˫����y��![]() �ڵ�һ�����ڵĽ��㣬PB��x�ᣬ����Ϊ��B����OB��2��PB��4��
�ڵ�һ�����ڵĽ��㣬PB��x�ᣬ����Ϊ��B����OB��2��PB��4��
��1�����������Ľ���ʽ��
��2�����APB�������
��3�����ڵ�һ�����ڣ���xȡ��ֵʱһ�κ�����ֵС�ڷ�����������ֵ��
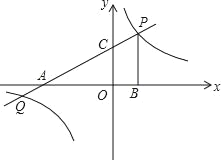
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
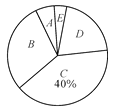
����Ŀ����ɽ������һ�ֳ����������ɫˮ�����������һ�֣���Ϊ��������ɽ�ض�����������20����ɽ���棬��ÿ��25ǧ�˵�����Ϊ�������������ǧ�����ֱ���������������ʾ����¼���£�

(1)��20����ɽ�����У����ص�һ��������һ���ض���ǧ�ˣ�
(2)��������Ƚϣ���20����ɽ�����ܼƳ����������ǧ�ˣ�
(3)����ɽ����ÿǧ���ۼ�4Ԫ������20����ɽ�����������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��������̻�������˾�����Ƴ���У�̻�����������շѷ�����
��˾������ÿ�µ���������y��Ԫ�����̻����x��ƽ���ף��Ĺ�ϵ��ͼ��ʾ��
�ҹ�˾�������̻����������1000ƽ����ʱ��ÿ����ȡ����5500Ԫ���̻��������1000ƽ����ʱ�������IJ���ÿ��ÿƽ������4Ԫ��
��1������ͼ��ʾ��y��x�ĺ�������ʽ��
��2�����ijѧУĿǰ���̻������1200ƽ���ף���ôѡ���ļҹ�˾�ķ���Ƚϻ��㣮
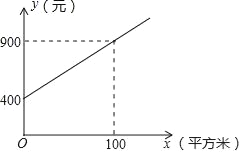
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���֪������y=ax2+bx��5��x�ύ��A����1��0����B��5��0�����㣬��y�ύ�ڵ�C��
��1���������ߵĺ�������ʽ��
��2����ͼ2��CE��x�����������ཻ�ڵ�E����H��ֱ��CE�·��������ϵĶ��㣬����H����y��ƽ�е�ֱ����BC��CE�ֱ��ཻ�ڵ�F��G����̽������H�˶����δ�ʱ���ı���CHEF�����������H�����ꣻ
��3������KΪ�����ߵĶ��㣬��M��4��m���Ǹ��������ϵ�һ�㣬��x�ᣬy���Ϸֱ��ҵ�P��Q��ʹ�ı���PQKM���ܳ���С�������P��Q�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=![]() +bx+c��a��0���IJ���ͼ����ͼ��ʾ��ͼ����㣨��1��0�����Գ���Ϊֱ��x=2�����н��ۣ���1��4a+b=0����2��9a+c��3b����3��8a+7b+2c��0����4������A����3��
+bx+c��a��0���IJ���ͼ����ͼ��ʾ��ͼ����㣨��1��0�����Գ���Ϊֱ��x=2�����н��ۣ���1��4a+b=0����2��9a+c��3b����3��8a+7b+2c��0����4������A����3��![]() ������B��
������B��![]() ��
��![]() ������C��
������C��![]() ��
��![]() ���ڸú���ͼ���ϣ���
���ڸú���ͼ���ϣ���![]() ��
��![]() ��
��![]() ����5��������a��x+1����x��5��=��3������Ϊ
����5��������a��x+1����x��5��=��3������Ϊ![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ����1��5��
����1��5��![]() ��������ȷ�Ľ����У� ��.
��������ȷ�Ľ����У� ��.

A��2�� B��3�� C��4�� D��5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC��ֱ������ϵ�У�

��1����д����ABC��������꣮
��2�������ABC�������
��3�����ѡ�ABC����ƽ��2����λ��������ƽ��2����λ�õ���A��B��C�䣬����ͼ�л�����A��B��C�䣬��д����A�䡢B�䡢C������꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com