
【题目】为发展旅游经济,我市某景区对门票采用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分的游客打b折售票.设某旅游团人数为x人,非节假日购票款为![]() (元),节假日购票款为
(元),节假日购票款为![]() (元).
(元).![]() ,
,![]() 与x之间的函数图象如图所示.
与x之间的函数图象如图所示.
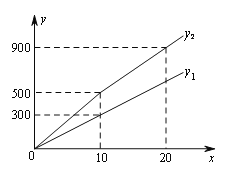
(1)观察图象可知:a= ;b= ;m= ;
(2)直接写出![]() ,
,![]() 与x之间的函数关系式;
与x之间的函数关系式;
(3)某旅行社导游王娜于5月1日带A团,5月20日(非节假日)带B团都到该景区旅游,共付门票款1900元,A,B两个团队合计50人,求A,B两个团队各有多少人?
【答案】(1)门票定价为50元/人,那么10人应花费500元,而从图可知实际只花费300元,是打6折得到的价格,
所以a=6;
从图可知10人之外的另10人花费400元,而原价是500元,可以知道是打8折得到的价格,
所以b=8,
看图可知m=10;
(2)设y1=kx,当x=10时,y1=300,代入其中得, k=30.
y1的函数关系式为:y1=30x,
同理可得,y2=50x(0≤x≤10),
当x>10时,设其解析式为:y2=(x-10)×50×0.8+500,
化简得:y2=40x+100;
(3)设A团有n人,则B团有(50-n)人,
当0≤n≤10时,50n+30(50-n)=1900解得,
n=20这与n≤10矛盾,
当n>10时,40n+100+30(50-n)=1900,
解得,n=30,50-30=20.
答:A团有30人,B团有20人.
【解析】试题分析:(1)根据原票价和实际票价可求a、b的值,m的值可看图得到;
(2)先列函数解析式,然后将图形中的对应值代入其中求出常数项,即可得到解析式;
(3)分两种情况讨论,即不多于10和多于10人,找出等量关系,列出关于人数n的一元一次方程,解此可得人数.
试题解析:解:(1)门票定价为50元/人,那么10人应花费500元,而从图可知实际只花费300元,是打6折得到的价格,所以a=6;
从图可知10人之外的另10人应花费400元,而原价是500元,可以知道是打8折得到的价格,所以b=8,可图可知m=10;
(2)![]() ;
; 
(3)设A团有n人,则B团有(50-n)人,
当0≤n≤10时,50n+30(50-n)=1900,
解之,得n=20,这与n≤10矛盾,
40n+100+30(50-n)=1900,
解之,得n=30,
50-30=20,
答:A团有30人,B团有20人。


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】砀山酥梨是一种驰名中外的特色水果,它是梨的一种,因为出产于砀山县而得名。现有20筐砀山酥梨,以每筐25千克的质量为标准,超过或不足的千克数分别用正、负数来表示,记录如下:

(1)这20筐砀山酥梨中,最重的一筐比最轻的一筐重多少千克?
(2)与标准质量比较,这20筐砀山酥梨总计超过或不足多少千克?
(3)若砀山酥梨每千克售价4元,则这20筐砀山酥梨可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
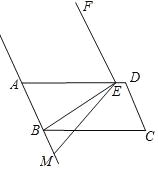
【题目】如图,四边形ABCD为平行四边形,过点B作BE⊥AB交AD于点E,将线段BE绕点E顺时针旋转90°到EF的位置,点M(点M不与点B重合)在直线AB上,连结EM.
(1)当点M在线段AB的延长线上时,将线段EM绕点E顺时针旋转90°到EN1的位置,连结FN1,在图中画出图形,求证:FN1⊥AB;
(2)当点M在线段BA的延长线上时,将线段EM绕点E顺时针旋转90°到EN2的位置,连结FN2,在图中画出图形,点N2在直线FN1上吗?请说明理由;
(3)若AB=3,AD=6,DE=1,设BM=x,在(1)、(2)的条件下,试用含x的代数式表示△FMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
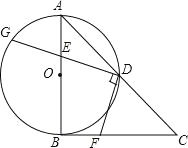
(1)求证:AE=BF;
(2)连接GB,EF,求证:GB∥EF;
(3)若AE=1,EB=2,求DG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)某商场统计了今年1~5月A,B两种品牌冰箱的销售情况,并将获得的数据绘制成折线统计图.
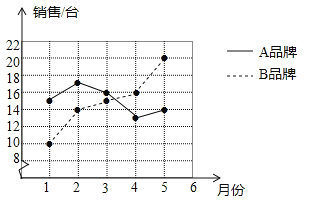
(1)分别求该商场这段时间内A,B两种品牌冰箱月销售量的中位数和方差;
(2)根据计算结果,比较该商场1~5月这两种品牌冰箱月销售量的稳定性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,

(1)请写出△ABC各点的坐标.
(2)求出△ABC的面积.
(3)若把△ABC向上平移2个单位,再向右平移2个单位得到△A′B′C′,请在图中画出△A′B′C′,并写出点A′、B′、C′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防流感,某学校在星期天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(小时)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据以上信息解答下列问题:
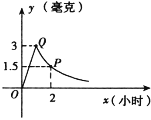
(1)求药物释放完毕后,y与x之间的函数关系式并写出自变量的取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进入教室,那么,从星期天下午5:00开始对某教室释放药物进行消毒,到星期一早上7:00时学生能否进入教室?
查看答案和解析>>
科目:初中数学 来源: 题型:
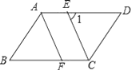
【题目】如图,在ABCD中,CE平分∠BCD,且交AD于点E,AF∥CE,且交BC于点F.
(1)求证:△ABF≌△CDE;
(2)如图,若∠B=52°,求∠1的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某面粉厂从生产的袋装面粉中抽出样品20袋,检测每袋的质量是否符合标准,超过、不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值(单位:千克) | -0.3 | -0.2 | -0.1 | 0 | 0.1 | 0.2 |
袋数 | 3 | 2 | 4 | 6 | 3 | 2 |
(1)这批样品中最多的一袋比最少的一袋多多少千克?
(2)这20袋面粉的总质量比标准的质量多(或少)多少千克?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com