
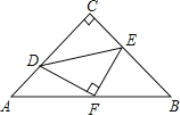
【题目】如图,已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD,FE分别交AC,BC于点D,E两点,当∠DFE在△ABC内绕顶点F旋转时(点D不与A,C重合),给出以下个结论:①CD=BE;②四边形CDFE不可能是正方形;③△DFE是等腰直角三角形;④S四边形CDFE=![]() S△ABC.上述结论中始终正确的有______.(填序号)
S△ABC.上述结论中始终正确的有______.(填序号)
【答案】①③④
【解析】
首先连接CF,由等腰直角三角形的性质可得:![]() ,则证得∠DCF=∠B,∠DFC=∠EFB,然后可证得:△DCF≌△EBF,由全等三角形的性质可得CD=BE,DF=EF,也可证得S四边形CDFE=
,则证得∠DCF=∠B,∠DFC=∠EFB,然后可证得:△DCF≌△EBF,由全等三角形的性质可得CD=BE,DF=EF,也可证得S四边形CDFE=![]() S△ABC.问题得解.
S△ABC.问题得解.
解:连接CF,
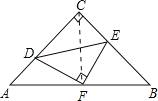
∵AC=BC,∠ACB=90°,点F是AB中点,
![]()
∴∠DCF=∠B=45°,
∵∠DFE=90°,
∴∠DFC+∠CFE=∠CFE+∠EFB=90°,
∴∠DFC=∠EFB,
∴△DCF≌△EBF,
∴CD=BE,故①正确;
∴DF=EF,
∴△DFE是等腰直角三角形,故③正确;
∴S△DCF=S△BEF,
∴S四边形CDFE=S△CDF+S△CEF=S△EBF+S△CEF=S△CBF=![]() S△ABC.,故④正确.
S△ABC.,故④正确.
若EF⊥BC时,则可得:四边形CDFE是矩形,
∵DF=EF,
∴四边形CDFE是正方形,故②错误.
∴结论中始终正确的有①③④.
故答案为:①③④.


科目:初中数学 来源: 题型:
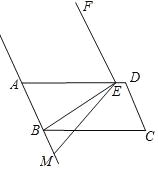
【题目】如图,四边形ABCD为平行四边形,过点B作BE⊥AB交AD于点E,将线段BE绕点E顺时针旋转90°到EF的位置,点M(点M不与点B重合)在直线AB上,连结EM.
(1)当点M在线段AB的延长线上时,将线段EM绕点E顺时针旋转90°到EN1的位置,连结FN1,在图中画出图形,求证:FN1⊥AB;
(2)当点M在线段BA的延长线上时,将线段EM绕点E顺时针旋转90°到EN2的位置,连结FN2,在图中画出图形,点N2在直线FN1上吗?请说明理由;
(3)若AB=3,AD=6,DE=1,设BM=x,在(1)、(2)的条件下,试用含x的代数式表示△FMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防流感,某学校在星期天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(小时)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据以上信息解答下列问题:
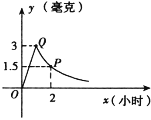
(1)求药物释放完毕后,y与x之间的函数关系式并写出自变量的取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进入教室,那么,从星期天下午5:00开始对某教室释放药物进行消毒,到星期一早上7:00时学生能否进入教室?
查看答案和解析>>
科目:初中数学 来源: 题型:
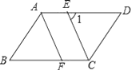
【题目】如图,在ABCD中,CE平分∠BCD,且交AD于点E,AF∥CE,且交BC于点F.
(1)求证:△ABF≌△CDE;
(2)如图,若∠B=52°,求∠1的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
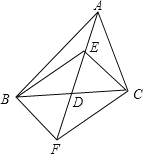
【题目】在△ABC 中,D 是 BC 边的中点,E、F 分别在 AD 及其延长线上,CE∥BF,连接BE、CF.
(1)求证:△BDF ≌△CDE;
(2)若 DE = BC,试判断四边形 BFCE 是怎样的四边形,并证明你的结论.
BC,试判断四边形 BFCE 是怎样的四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=.
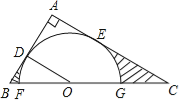
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某面粉厂从生产的袋装面粉中抽出样品20袋,检测每袋的质量是否符合标准,超过、不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值(单位:千克) | -0.3 | -0.2 | -0.1 | 0 | 0.1 | 0.2 |
袋数 | 3 | 2 | 4 | 6 | 3 | 2 |
(1)这批样品中最多的一袋比最少的一袋多多少千克?
(2)这20袋面粉的总质量比标准的质量多(或少)多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校初一年级参加社会实践课,报名第一门课的有x人,第二门课的人数比第一门课的![]() 少20人,现在需要从报名第二门课的人中调出10人学习第一门课,那么用含x的式子解答下题.
少20人,现在需要从报名第二门课的人中调出10人学习第一门课,那么用含x的式子解答下题.
(1)报两门课的共有多少人?
(2)调动后,报名第一门课比报名第二门课多多少人?计算出代数式后,请选择一个你觉得合适的x值代入,并求出具体人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com