
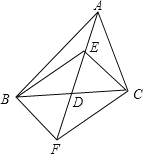
【题目】在△ABC 中,D 是 BC 边的中点,E、F 分别在 AD 及其延长线上,CE∥BF,连接BE、CF.
(1)求证:△BDF ≌△CDE;
(2)若 DE = BC,试判断四边形 BFCE 是怎样的四边形,并证明你的结论.
BC,试判断四边形 BFCE 是怎样的四边形,并证明你的结论.
【答案】见解析
【解析】
(1)由已知条件易得∠CED=∠BFD,BD=CD,结合∠BDF=∠CDE即可证得:△BDF≌△CDE;
(2)由△BDF≌△CDE易得DE=DF,结合BD=CD可得四边形BFCE是平行四边形,结合DE= BC可得EF=BC,由此即可证得平行四边形BFCE是矩形.
BC可得EF=BC,由此即可证得平行四边形BFCE是矩形.
(1)∵CE∥BF,
∴∠CED=∠BFD.
∵D是BC边的中点,
∴BD=DC,
在△BDF和△CDE中, ,
,
∴△BDF≌△CDE(AAS).
(2)四边形BFCE是矩形.理由如下:
∵△BDF≌△CDE,
∴DE=DF,
又∵BD=DC,
∴四边形BFCE是平行四边形.
∵DE= BC,DE=
BC,DE= EF,
EF,
∴BC=EF,
∴平行四边形BFCE是矩形.


科目:初中数学 来源: 题型:
【题目】 “已知:正比例函数y1=kx(k>0)与反比例函数y2=![]() (m>0)图象相交于A、B两点,其横坐标分别是1和﹣1,求不等式kx>
(m>0)图象相交于A、B两点,其横坐标分别是1和﹣1,求不等式kx>![]() 的解集.”对于这道题,某同学是这样解答的:“由图象可知:当x>1或﹣1<x<0时,y1>y2,所以不等式kx>
的解集.”对于这道题,某同学是这样解答的:“由图象可知:当x>1或﹣1<x<0时,y1>y2,所以不等式kx>![]() 的解集是x>1或﹣1<x<0”.他这种解决问题的思路体现的数学思想方法是( )
的解集是x>1或﹣1<x<0”.他这种解决问题的思路体现的数学思想方法是( )
A.数形结合 B.转化 C.类比 D.分类讨论
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,已知AD∥BC,AB=DC,AD=2,BC=4,延长BC到E,使CE=AD.
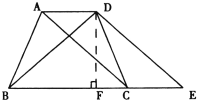
(1)写出图中所有与△DCE全等的三角形,并选择其中一对说明全等的理由;
(2)探究:当梯形ABCD的高DF等于多少时,对角线AC与BD互相垂直?请回答并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和同学一起去书店买书,他们先用60元买了一种科普书,又用60元买了一种文学书.科普书的价格比文学书高出一半,他们所买的科普书比所买的文学书少2本.
(1)求他们买的科普书和文学书的价格各是多少元?
(2)学校某月开展读书活动,班上同学让小颖帮助购买科普书和文学书共20本,且购买总费用不超过260元,求小颖至少购买多少本文学书?
查看答案和解析>>
科目:初中数学 来源: 题型:
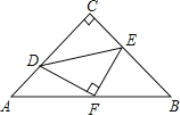
【题目】如图,已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD,FE分别交AC,BC于点D,E两点,当∠DFE在△ABC内绕顶点F旋转时(点D不与A,C重合),给出以下个结论:①CD=BE;②四边形CDFE不可能是正方形;③△DFE是等腰直角三角形;④S四边形CDFE=![]() S△ABC.上述结论中始终正确的有______.(填序号)
S△ABC.上述结论中始终正确的有______.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
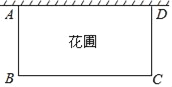
【题目】为了美化生活环境,小兰的爸爸要在院墙外的一块空地上修建一个矩形花圃.如图所示,矩形花圃的一边利用长10米的院墙,另外三条边用篱笆围成,篱笆的总长为32米.设AB的长为x米,矩形花圃的面积为y平方米.
(1)用含有x的代数式表示BC的长,BC= ;
(2)求y与x的函数关系式,写出自变量x的取值范围;
(3)当x为何值时,y有最大值?最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】徐州地铁1号线,西起杏山子大道,止于高铁徐州东站,共设18座站点,18座站点如下所示.徐州轨道交通试运营期间,小苏从苏堤路站开始乘坐地铁,在地铁各站点做志愿者服务,到![]() 站下车时,本次志愿者服务活动结束,约定向徐州东站站方向(即箭头方向)为正,当天的乘车记录如下(单位:站):
站下车时,本次志愿者服务活动结束,约定向徐州东站站方向(即箭头方向)为正,当天的乘车记录如下(单位:站):![]() ,-2,-6,
,-2,-6,![]() 8,
8,![]() 3,-4,-9,
3,-4,-9,![]() 8.
8.


(1)请通过计算说明![]() 站是哪一站?
站是哪一站?
(2)如果相邻两站之间的距离为![]() 千米,求这次小苏志愿服务期间乘坐地铁行进的总路程是多少千米?
千米,求这次小苏志愿服务期间乘坐地铁行进的总路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表8.
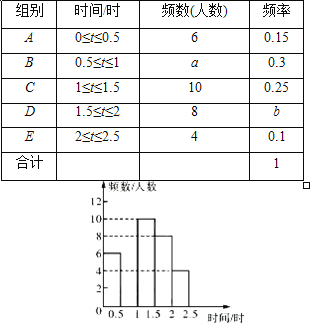
请根据图表中的信息,解答下列问题:
(1)表中的a=______,b=______,中位数落在________组,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有多少名?
(3)E组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出2人向全校同学作读书心得报告,请用画树状图或列表法求抽取的2名学生刚好是1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() ,
,![]() ,
,![]() ,点
,点![]() 与
与![]() 关于
关于![]() 轴对称.
轴对称.
(1)写出点![]() 所在直线的函数解析式;
所在直线的函数解析式;
(2)连接![]() ,若线段
,若线段![]() 能构成三角形,求
能构成三角形,求![]() 的取值范围;
的取值范围;
(3)若直线![]() 把四边形
把四边形![]() 的面积分成相等的两部分,试求
的面积分成相等的两部分,试求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com