【题目】徐州地铁1号线，西起杏山子大道，止于高铁徐州东站，共设18座站点，18座站点如下所示.徐州轨道交通试运营期间，小苏从苏堤路站开始乘坐地铁，在地铁各站点做志愿者服务，到
站下车时，本次志愿者服务活动结束，约定向徐州东站站方向（即箭头方向）为正，当天的乘车记录如下（单位：站）：
，-2，-6，
8，3，-4，-9，8.
（1）请通过计算说明站是哪一站？
（2）如果相邻两站之间的距离为
千米，求这次小苏志愿服务期间乘坐地铁行进的总路程是多少千米？
名校课堂系列答案科目：初中数学 来源： 题型：
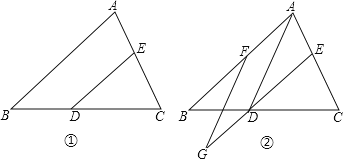
【题目】已知：点D，E分别是△ABC的BC，AC边的中点.
(1)如图①，若AB=10，求DE的长；
(2)如图②,点F是AB边上的一点,FG//AD,交ED的延长线于点G.求证：AF=DG
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，观察由棱长为 
的小立方体摆成的图形，寻找规律：如图 ① 中，共有 
个小立方体，其中 
个看得见， 
个看不见；如图 ② 中，共有 
个小立方体，其中 
个看得见， 
个看不见；如图 ③ 中，共有 
个小立方体，其中 
个看得见， 
个看不见； 
，则第 ⑥个图中，看得见的小立方体有________________个．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，杭州某化工厂与A，B两地有公路，铁路相连．这家工厂从A地购买一批每吨1000元的原料运回工厂，制成每吨8000元的产品运到B地．已知公路运价为1.4元/（吨千米），铁路运价为1.1元/（吨千米），且这两次运输共支出公路运输费14000元，铁路运输费89100元，求：
（1）该工厂从A地购买了多少吨原料？制成运往B地的产品多少吨？
（2）这批产品的销售款比原料费与运输费的和多多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下列两个等式：2
=2×+1，5
=5×+1，给出定义如下：我们称使等式ab＝ab＋1的成立的一对有理数a，b为“共生有理数对”，记为（a，b），如：数对（2，），（5，），都是“共生有理数对”．
(1)判断数对(2,1),(3,
)是不是“共生有理数对”，写出过程；
(2)若(a,3)是“共生有理数对”，求a的值；
(3)若(m,n)是“共生有理数对”,则(n,m)“共生有理数对”(填“是”或“不是”)；说明理由；
(4)请再写出一对符合条件的“共生有理数对”为(注意：不能与题目中已有的“共生有理数对”重复).
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AB为⊙O的直径，点E在⊙O上，∠EAB的平分线交⊙O于点C，过点C作AE的垂线，垂足为D，直线DC与AB的延长线交于点P．
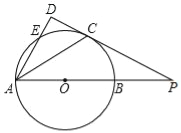
（1）判断直线PC与⊙O的位置关系，并说明理由；
（2）若tan∠P=
，AD=6，求线段AE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
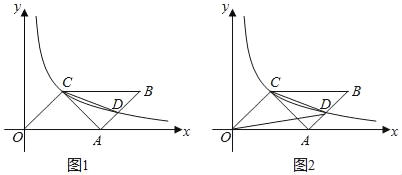
【题目】如图1，在平面直角坐标系中，OABC的一个顶点与坐标原点重合，OA边落在x轴上，且OA=4，OC=2
，∠COA=45°．反比例函数y=
（k＞0，x＞0）的图象经过点C，与AB交于点D，连接AC，CD．
（1）试求反比例函数的解析式；
（2）求证：CD平分∠ACB；
（3）如图2，连接OD，在反比例的函数图象上是否存在一点P，使得S△POC=
S△COD？如果存在，请直接写出点P的坐标．如果不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下表给出了1班6名学生的身高情况与全班平均身高的差值（单位：厘米）
学生 | A | B | C | D | E | F |
身高 | 157 | 162 | 159 | 152 | 163 | 164 |
身高与全班平均身高的差值 | -3 | +2 | -1 | a | +3 | b |
（1）列式计算表中数据a和b
（2）这6名学生的平均身高与全班学生的平均身高相比，在数值上有什么关系？（通过计算回答）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
