
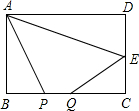
 如图,矩形ABCD中,AB=8,BC=16,E为CD的中点,点P、Q为BC上两个动点,
如图,矩形ABCD中,AB=8,BC=16,E为CD的中点,点P、Q为BC上两个动点,分析 ①延长AB到M,使BM=AB,则A和M关于BC对称,连接EM交BC于P,此时AP+EP的值最小,作作EN⊥AB,根据勾股定理求出EM长;
②点A向右平移3个单位到M,点E关于BC的对称点F,连接MF,交BC于Q,要使四边形APQE的周长最小,只要AP+EQ最小就行,证△MNQ∽△FCQ即可.
解答 解:①如图1,延长AB到M,使BM=AB=8,则A和M关于BC对称,连接EM交BC于P,此时AP+EP的值最小,AP+PE=EM,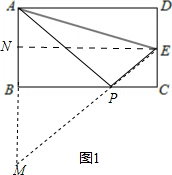
作EN⊥AB,
∴EN=AD=16,BN=$\frac{1}{2}$AB=4,BM=AB=8,
∴MN=12,
∴EM=$\sqrt{E{N}^{2}+M{N}^{2}}$=$\sqrt{1{6}^{2}+1{2}^{2}}$=20.
②如图2,点A向右平移6个单位到M,点E关于BC的对称点F,连接MF,交BC于Q,此时MQ+EQ最小,
∴要使四边形APQE的周长最小,只要AP+EQ最小就行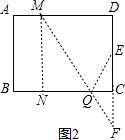 ,
,
即AP+EQ=MQ+EQ过M作MN⊥BC于N,
设CQ=x,则NQ=16-6-x=10-x,
∵△MNQ∽△FCQ,
∴$\frac{MN}{CF}=\frac{NQ}{CQ}$,
∵MN=AB=8,CF=CE=4,CQ=x,QN=10-x,
解得:x=$\frac{10}{3}$.
故答案为:$\frac{10}{3}$.
点评 本题考查了矩形的性质,勾股定理,轴对称-最短路线问题的应用,题目具有一定的代表性,但是一道难度偏大的题目,对学生提出较高的要求.


科目:初中数学 来源: 题型:解答题
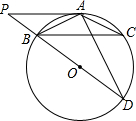 如图,⊙O是△ABC 的外接圆,AB=AC,BD是⊙O的直径,PA∥BC,与DB的延长线交于点P,连接AD.
如图,⊙O是△ABC 的外接圆,AB=AC,BD是⊙O的直径,PA∥BC,与DB的延长线交于点P,连接AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
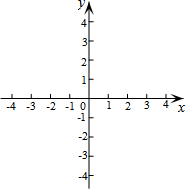 如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(-1,3),B(-3,2),C(0,1).画出△ABC,并画出关于原点O对称的△A1B1C1.
如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(-1,3),B(-3,2),C(0,1).画出△ABC,并画出关于原点O对称的△A1B1C1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
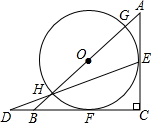 如图,在等腰直角三角形△ABC中,∠ACB=90°,以斜边AB上的点O为圆心的圆分别与AC、BC相切于E、F,与AB分别交于点G、H,且EH的延长线和CB的延长线交于点D.
如图,在等腰直角三角形△ABC中,∠ACB=90°,以斜边AB上的点O为圆心的圆分别与AC、BC相切于E、F,与AB分别交于点G、H,且EH的延长线和CB的延长线交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
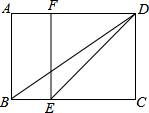 已知:如图,在矩形ABCD中,E是BC边上一点,DE平分∠ADC,EF∥DC交AD边于点F,连结BD.
已知:如图,在矩形ABCD中,E是BC边上一点,DE平分∠ADC,EF∥DC交AD边于点F,连结BD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm).现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升$\frac{5}{6}$cm,则开始注入$\frac{3}{5}$,$\frac{33}{20}$,$\frac{171}{40}$分钟的水量后,甲与乙的水位高度之差是0.5cm.
实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm).现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升$\frac{5}{6}$cm,则开始注入$\frac{3}{5}$,$\frac{33}{20}$,$\frac{171}{40}$分钟的水量后,甲与乙的水位高度之差是0.5cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 正方形A1B1C1O和A2B2C2C1按如图所示方式放置,点A1,A2在直线y=x+1上,点C1,C2在x轴上.已知A1点的坐标是(0,1),则点B2的坐标为(3,2).
正方形A1B1C1O和A2B2C2C1按如图所示方式放置,点A1,A2在直线y=x+1上,点C1,C2在x轴上.已知A1点的坐标是(0,1),则点B2的坐标为(3,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com