
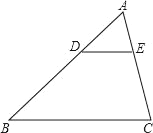
【题目】如图,已知△ABC∽△ADE,AB=30cm,BD=18cm,BC=20cm,∠BAC=75°,∠ABC=40°.
求:(1)∠ADE和∠AED的度数;
(2)DE的长.
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场有一个可以自由转动的圆形转盘(如图).规定:顾客购物100元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品(指针指向两个扇形的交线时,当作指向右边的扇形).下表是活动进行中的一组统计数据:
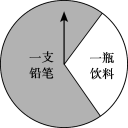
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 546 | 701 |
落在“铅笔”的频率 (结果保留小数点后两位) | 0.68 | 0.74 | 0.68 | 0.69 | 0.68 | 0.70 |
(1)转动该转盘一次,获得铅笔的概率约为_______;(结果保留小数点后一位)
(2)铅笔每只0.5元,饮料每瓶3元,经统计该商场每天约有4000名顾客参加抽奖活动,请计算该商场每天需要支出的奖品费用;
(3)在(2)的条件下,该商场想把每天支出的奖品费用控制在3000元左右,则转盘上“一瓶饮料”区域的圆心角应调整为______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某生利用标杆测量学校旗杆的高度,标杆CD等于3m,标杆与旗杆的水平距离BD=15m,人的眼睛距地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m.则旗杆AB的高度为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,按照下列操作作图:①以A为圆心,AC长为半径画弧交AD的延长线于点E;②以E为圆心,EC长为半径画弧交DE的延长线于点F;③分别以C,F为圆心,大于![]() CF的长为半径画弧,两弧相交于点N;④作射线EN,根据作图,若∠ACB=72°,则∠FEN的度数为( )
CF的长为半径画弧,两弧相交于点N;④作射线EN,根据作图,若∠ACB=72°,则∠FEN的度数为( )
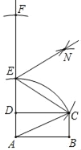
A. 54° B. 63° C. 72° D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
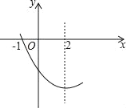
【题目】抛物线y=ax2+bx+c(a≠0)图象的一部分如图所示,其对称轴为x=2,与x轴的一个交点是(﹣1,0),有以下结论:①abc>0;②4a﹣2b+c<0;③4a+b=0④抛物线与x轴的另一个交点是(5,0)⑤若点(﹣3,y1)(﹣6,y2)都在抛物线上,则y1<y2.其中正确的是_____.(只填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线y=x2﹣3x+c与y轴的交点为(0,2),则下列说法正确的是( )
A. 抛物线开口向下
B. 抛物线与x轴的交点为(﹣1,0),(3,0)
C. 当x=1时,y有最大值为0
D. 抛物线的对称轴是直线x=![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com