
ЁОЬтФПЁПФГЩЬГЁгавЛИіПЩвдздгЩзЊЖЏЕФдВаЮзЊХЬЃЈШчЭМЃЉЃЎЙцЖЈЃКЙЫПЭЙКЮя100дЊвдЩЯПЩвдЛёЕУвЛДЮзЊЖЏзЊХЬЕФЛњЛсЃЌЕБзЊХЬЭЃжЙЪБЃЌжИеыТфдкФФвЛИіЧјгђОЭЛёЕУЯргІЕФНБЦЗЃЈжИеыжИЯђСНИіЩШаЮЕФНЛЯпЪБЃЌЕБзїжИЯђгвБпЕФЩШаЮЃЉЃЎЯТБэЪЧЛюЖЏНјаажаЕФвЛзщЭГМЦЪ§ОнЃК
зЊЖЏзЊХЬЕФДЮЪ§n | 100 | 150 | 200 | 500 | 800 | 1000 |
ТфдкЁАЧІБЪЁБЕФДЮЪ§m | 68 | 111 | 136 | 345 | 546 | 701 |
ТфдкЁАЧІБЪЁБЕФЦЕТЪ ЃЈНсЙћБЃСєаЁЪ§ЕуКѓСНЮЛЃЉ | 0.68 | 0.74 | 0.68 | 0.69 | 0.68 | 0.70 |
ЃЈ1ЃЉзЊЖЏИУзЊХЬвЛДЮЃЌЛёЕУЧІБЪЕФИХТЪдМЮЊ_______ЃЛЃЈНсЙћБЃСєаЁЪ§ЕуКѓвЛЮЛЃЉ
ЃЈ2ЃЉЧІБЪУПжЛ0.5дЊЃЌвћСЯУПЦП3дЊЃЌОЭГМЦИУЩЬГЁУПЬьдМга4000УћЙЫПЭВЮМгГщНБЛюЖЏЃЌЧыМЦЫуИУЩЬГЁУПЬьашвЊжЇГіЕФНБЦЗЗбгУЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌИУЩЬГЁЯыАбУПЬьжЇГіЕФНБЦЗЗбгУПижЦдк3000дЊзѓгвЃЌдђзЊХЬЩЯЁАвЛЦПвћСЯЁБЧјгђЕФдВаФНЧгІЕїећЮЊ______ЖШЃЎ
ЁОД№АИЁПЃЈ1ЃЉ0.7ЃЛЃЈ2ЃЉИУЩЬГЁУПЬьДѓжТашвЊжЇГіЕФНБЦЗЗбгУЮЊ5000дЊЃЛЃЈ3ЃЉ36
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУЦЕТЪЙРМЦИХТЪЧѓНтЃЛ
ЃЈ2ЃЉРћгУЃЈ1ЃЉЕУЕНЛёЕУЧІБЪЕФИХТЪЮЊ0.7КЭЛёЕУвћСЯЕФИХТЪЮЊ0.3ЃЌШЛКѓМЦЫу4000ЁС0.5ЁС0.7+4000ЁС3ЁС0.3МДПЩЃЛ
ЃЈ3ЃЉЩшзЊХЬЩЯЁАвЛЦПвћСЯЁБЧјгђЕФдВаФНЧгІЕїећЮЊnЖШЃЌдђ4000ЁС3ЁС![]() +4000ЁС0.5ЃЈ1-
+4000ЁС0.5ЃЈ1-![]() ЃЉ=3000ЃЌШЛКѓНтЗНГЬМДПЩЃЎ
ЃЉ=3000ЃЌШЛКѓНтЗНГЬМДПЩЃЎ
ЃЈ1ЃЉзЊЖЏИУзЊХЬвЛДЮЃЌЛёЕУЧІБЪЕФИХТЪдМЮЊ0.7ЃЛ
ЙЪД№АИЮЊ: 0.7
ЃЈ2ЃЉ4000ЁС0.5ЁС0.7+4000ЁС3ЁС0.3ЃН5000ЃЌ
ЫљвдИУЩЬГЁУПЬьДѓжТашвЊжЇГіЕФНБЦЗЗбгУЮЊ5000дЊЃЛ
ЃЈ3ЃЉЩшзЊХЬЩЯЁАвЛЦПвћСЯЁБЧјгђЕФдВаФНЧгІЕїећЮЊnЖШЃЌ
дђ4000ЁС3ЁС![]() +4000ЁС0.5ЃЈ1Љ
+4000ЁС0.5ЃЈ1Љ![]() ЃЉЃН3000ЃЌНтЕУnЃН36ЃЌ
ЃЉЃН3000ЃЌНтЕУnЃН36ЃЌ
ЫљвдзЊХЬЩЯЁАвЛЦПвћСЯЁБЧјгђЕФдВаФНЧгІЕїећЮЊ36ЖШЃЎ
ЙЪД№АИЮЊ36ЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
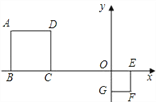
ЁОЬтФПЁПе§ЗНаЮABCDгые§ЗНаЮOEFGжаЃЌЕуDКЭЕуFЕФзјБъЗжБ№ЮЊЃЈЉ3ЃЌ2ЃЉКЭЃЈ1ЃЌЉ1ЃЉЃЌдђетСНИіе§ЗНаЮЕФЮЛЫЦжааФЕФзјБъЮЊ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
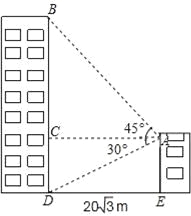
ЁОЬтФПЁПаЁУєМвЖдУцаТНЈСЫвЛДБЭМЪщДѓЯУЃЌаЁУєдкздМвДАПкВтЕУДѓЯУЖЅВПЕФбіНЧЮЊ45ЁуЃЌДѓЯУЕзВПЕФбіНЧЮЊ30ЁуЃЌШчЭМЫљЪОЃЌСПЕУСНДБТЅжЎМфЕФОрРыЮЊ20![]() УзЃЎ
УзЃЎ
ЃЈ1ЃЉЧѓГіДѓЯУЕФИпЖШBDЃЛ
ЃЈ2ЃЉЧѓГіаЁУєМвЕФИпЖШAEЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЫФБпаЮABCDЮЊСтаЮЃЌЧвAЃЈ0ЃЌ4ЃЉЁЂDЃЈ3ЃЌ0ЃЉЃЎ
ЃЈ1ЃЉЧѓОЙ§ЕуCЕФЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшPЪЧЃЈ1ЃЉжаЫљЧѓКЏЪ§ЭМЯѓЩЯвЛЕуЃЌвдPЁЂOЁЂAЖЅЕуЕФШ§НЧаЮЕФУцЛ§гыЁїCOBЕФУцЛ§ЯрЕШЃЎЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпABКЭХзЮяЯпЕФНЛЕуЪЧA(0ЃЌ-3)ЃЌB(5ЃЌ9)ЃЌвбжЊХзЮяЯпЕФЖЅЕуDЕФКсзјБъЪЧ2.

(1)ЧѓХзЮяЯпЕФНтЮіЪНМАЖЅЕузјБъЃЛ
(2)дк![]() жсЩЯЪЧЗёДцдквЛЕуCЃЌгыAЃЌBзщГЩЕШбќШ§НЧаЮЃПШєДцдкЃЌЧѓГіЕуCЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
жсЩЯЪЧЗёДцдквЛЕуCЃЌгыAЃЌBзщГЩЕШбќШ§НЧаЮЃПШєДцдкЃЌЧѓГіЕуCЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
(3)дкжБЯпABЕФЯТЗНХзЮяЯпЩЯеввЛЕуPЃЌСЌНгPAЃЌPBЪЙЕУЁїPABЕФУцЛ§зюДѓЃЌВЂЧѓГіетИізюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
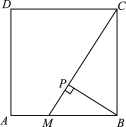
ЁОЬтФПЁПMЪЧе§ЗНаЮABCDЕФБпABЩЯвЛЖЏЕуЃЈВЛгыAЃЌBжиКЯЃЉЃЌBPЁЭMCЃЌДЙзуЮЊPЃЌНЋЁЯCPBШЦЕуPа§зЊЃЌЕУЕНЁЯCЁЏPBЁЏЃЌЕБЩфЯпPCЁЏОЙ§ЕуDЪБЃЌЩфЯпPBЁЏгыBCНЛгкЕуNЃЎ
ЃЈ1ЃЉвРЬтвтВЙШЋЭМаЮЃЛ
ЃЈ2ЃЉЧѓжЄЃКЁїBPNЁзЁїCPDЃЛ
ЃЈ3ЃЉдкЕуMЕФдЫЖЏЙ§ГЬжаЃЌЭМжаЪЧЗёДцдкгыBMЪМжеБЃГжЯрЕШЕФЯпЖЮЃПШєДцдкЃЌЧыаДГіетЬѕЯпЖЮВЂжЄУїЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮ ![]() ЪЧСтаЮЃЌ
ЪЧСтаЮЃЌ![]() B=6ЃЌЧвЁЯABC=60Ёу ЃЌMЪЧСтаЮФкШЮвЛЕуЃЌСЌНгAMЃЌBMЃЌCMЃЌдђAM+BM+CM ЕФзюаЁжЕЮЊ________ЁЃ
B=6ЃЌЧвЁЯABC=60Ёу ЃЌMЪЧСтаЮФкШЮвЛЕуЃЌСЌНгAMЃЌBMЃЌCMЃЌдђAM+BM+CM ЕФзюаЁжЕЮЊ________ЁЃ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
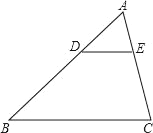
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCЁзЁїADEЃЌABЃН30cmЃЌBDЃН18cmЃЌBCЃН20cmЃЌЁЯBACЃН75ЁуЃЌЁЯABCЃН40ЁуЃЎ
ЧѓЃКЃЈ1ЃЉЁЯADEКЭЁЯAEDЕФЖШЪ§ЃЛ
ЃЈ2ЃЉDEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
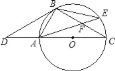
ЁОЬтФПЁПШчЭМЃЌЕуDЪЧЁбOЕФжБОЖCAбгГЄЯпЩЯвЛЕуЃЌЕуBдкЁбOЩЯЃЌЧвЁЯDBAЃНЁЯBCDЃЎ
ЃЈ1ЃЉИљОнФуЕФХаЖЯЃКBDЪЧЁбOЕФЧаЯпТ№ЃПЮЊЪВУДЃПЃЎ
ЃЈ2ЃЉШєЕуEЪЧСгЛЁBCЩЯвЛЕуЃЌAEгыBCЯрНЛгкЕуFЃЌЧвЁїBEFЕФУцЛ§ЮЊ10ЃЌcosЁЯBFAЃН![]() ЃЌФЧУДЃЌФуФмЧѓГіЁїACFЕФУцЛ§Т№ЃПШєФмЃЌЧыФуЧѓГіЦфУцЛ§ЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЃЌФЧУДЃЌФуФмЧѓГіЁїACFЕФУцЛ§Т№ЃПШєФмЃЌЧыФуЧѓГіЦфУцЛ§ЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com