
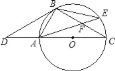
【题目】如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且∠DBA=∠BCD.
(1)根据你的判断:BD是⊙O的切线吗?为什么?.
(2)若点E是劣弧BC上一点,AE与BC相交于点F,且△BEF的面积为10,cos∠BFA=![]() ,那么,你能求出△ACF的面积吗?若能,请你求出其面积;若不能,请说明理由.
,那么,你能求出△ACF的面积吗?若能,请你求出其面积;若不能,请说明理由.
【答案】(1)BD是⊙O的切线,理由见解析;(2)见解析.
【解析】
(1)BD是⊙O的切线.先连接OB,由于AC是直径,那么∠ABC=90°,于是∠1+∠C=90°,而OA=OB,可得∠1=∠2,结合∠3=∠C,易得∠2+∠3=90°,从而可证DB是⊙O的切线;
(2)由于cos∠BFA=![]() ,那么
,那么![]() ,利用圆周角定理可知∠E=∠C,∠4=∠5,易证△EBF∽△CAF,于是
,利用圆周角定理可知∠E=∠C,∠4=∠5,易证△EBF∽△CAF,于是![]() ,从而易求△ACF的面积.
,从而易求△ACF的面积.
(1)BD是⊙O的切线.
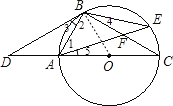
理由:如图所示,连接OB,
∵AC是⊙O的直径,
∴∠ABC=90°,
∴∠1+∠C=90°,
∵OA=OB,
∴∠1=∠2,
∴∠2+∠C=90°,
∵∠3=∠C,
∴∠2+∠3=90°,
∴DB是⊙O的切线;
(2)在Rt△ABF中,
∵cos∠BFA=![]() ,
,
∴![]() ,
,
∵∠E=∠C,∠4=∠5,
∴△EBF∽△CAF,
∴![]() ,
,
即![]() ,
,
解之得:S△ACF=22.5.


科目:初中数学 来源: 题型:
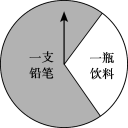
【题目】某商场有一个可以自由转动的圆形转盘(如图).规定:顾客购物100元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品(指针指向两个扇形的交线时,当作指向右边的扇形).下表是活动进行中的一组统计数据:
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 546 | 701 |
落在“铅笔”的频率 (结果保留小数点后两位) | 0.68 | 0.74 | 0.68 | 0.69 | 0.68 | 0.70 |
(1)转动该转盘一次,获得铅笔的概率约为_______;(结果保留小数点后一位)
(2)铅笔每只0.5元,饮料每瓶3元,经统计该商场每天约有4000名顾客参加抽奖活动,请计算该商场每天需要支出的奖品费用;
(3)在(2)的条件下,该商场想把每天支出的奖品费用控制在3000元左右,则转盘上“一瓶饮料”区域的圆心角应调整为______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
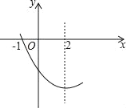
【题目】抛物线y=ax2+bx+c(a≠0)图象的一部分如图所示,其对称轴为x=2,与x轴的一个交点是(﹣1,0),有以下结论:①abc>0;②4a﹣2b+c<0;③4a+b=0④抛物线与x轴的另一个交点是(5,0)⑤若点(﹣3,y1)(﹣6,y2)都在抛物线上,则y1<y2.其中正确的是_____.(只填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线y=x2﹣3x+c与y轴的交点为(0,2),则下列说法正确的是( )
A. 抛物线开口向下
B. 抛物线与x轴的交点为(﹣1,0),(3,0)
C. 当x=1时,y有最大值为0
D. 抛物线的对称轴是直线x=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=mx2+(1﹣2m)x+1﹣3m(m是常数).
(Ⅰ)当m=1时,求该抛物线与x轴的公共点的坐标;
(Ⅱ)抛物线与x轴相交于不同的两点A,B.
①求m的取值范围;
②无论m取何值,该抛物线都经过非坐标轴上的定点P,当![]() <m≤8时,求△PAB面积的最大值,并求出相对应的m的值.
<m≤8时,求△PAB面积的最大值,并求出相对应的m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=![]() cm.
cm.
(1)求证:AC是⊙O的切线;
(2)求由弦CD、BD与弧BC所围成的阴影部分的面积.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
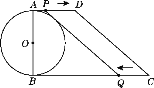
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=12 cm,AD=8 cm,BC=22 cm,AB为⊙O的直径,动点P从点A开始沿AD边向点D以1 cm/s的速度运动,动点Q从点C开始沿CB边向点B以2 cm/s的速度运动,P,Q分别从点A,C同时出发.当其中一动点到达终点时,另一个动点也随之停止运动.设运动时间为t s.当t为何值时,PQ与⊙O相切?
查看答案和解析>>
科目:初中数学 来源: 题型:
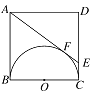
【题目】如图,正方形ABCD的边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com