
����Ŀ����ͼ�����ı���ABCD�У�AD��BC����ABC��90����AB��12 cm��AD��8 cm��BC��22 cm��ABΪ��O��ֱ��������P�ӵ�A��ʼ��AD�����D��1 cm/s���ٶ��˶�������Q�ӵ�C��ʼ��CB�����B��2 cm/s���ٶ��˶���P��Q�ֱ�ӵ�A��Cͬʱ������������һ���㵽���յ�ʱ����һ������Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt s����tΪ��ֵʱ��PQ����O���У�
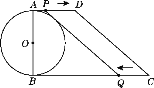
���𰸡���t��2s ʱ��PQ���O���У�
��������
��PQ��Բ������ʱ���������ߵ����ʰ�AP��PH��CQ��BQ�ֱ���t��ʾ��Ȼ�����ù��ɶ����Ϳ������t��
��PQ���O�����ڵ�H����P��PE��BC������ΪE��
��ֱ������ABCD��AD��BC����PE=AB��
��AP=BE=t��CQ=2t����BQ=BC��CQ=22��2t��EQ=BQ��BE=22��2t��t=22��3t��
��ABΪ��O��ֱ������ABC=��DAB=90�㣬��AD��BCΪ��O�����ߣ���AP=PH��HQ=BQ����PQ=PH+HQ=AP+BQ=t+22��2t=22��t��
��Rt��PEQ��PE2+EQ2=PQ2����122+��22��3t��2=��22��t��2������8t2��88t+144=0����t2��11t+18=0����t��2����t��9��=0����t1=2��t2=9��
��P��AD���˶���ʱ��Ϊ![]() �룮
�룮
��t=9��8����t=9����ȥ�����൱t=2��ʱ��PQ���O���У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı��� ![]() �����Σ�
�����Σ�![]() B=6���ҡ�ABC=60�� ��M����������һ�㣬����AM��BM��CM����AM+BM+CM ����СֵΪ________��
B=6���ҡ�ABC=60�� ��M����������һ�㣬����AM��BM��CM����AM+BM+CM ����СֵΪ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�������������Ž�����У���������������ʽ��A�����֣�B���赸��C�����У�D�����裮ÿ��ѧ������ѡ����ֻ��ѡ��һ����ϲ���ģ�ѧУ��������ʽ��ѧ�������˳������飬��������������������������������ͳ��ͼ��
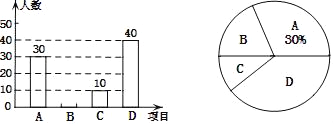
����ͼ��������Ϣ������������⣺
(1)���ε����ѧ������_____�ˣ�
(2)��ȫ����ͳ��ͼ��
(3)��У����1200��ѧ���������ѡ������������ѧ���ж����ˣ�
(4)����һ������ϲ������������ѧ���У��мס��ҡ���������λͬѧ�������㣬�ִ�����λͬѧ�����ѡ������ͬѧ�μ�ѧУ�����ֶӣ������б�����״ͼ����ѡȡ������ǡ���Ǽ��ҵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
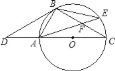
����Ŀ����ͼ����D�ǡ�O��ֱ��CA�ӳ�����һ�㣬��B�ڡ�O�ϣ��ҡ�DBA����BCD��
��1����������жϣ�BD�ǡ�O��������Ϊʲô����
��2������E���ӻ�BC��һ�㣬AE��BC�ཻ�ڵ�F������BEF�����Ϊ10��cos��BFA��![]() ����ô�����������ACF����������ܣ��������������������ܣ���˵�����ɣ�
����ô�����������ACF����������ܣ��������������������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
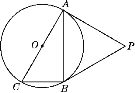
����Ŀ����ͼ����O��Rt��ABC�����Բ����ABC��90������P��Բ��һ�㣬PA����O�ڵ�A����PA��PB.
(1)��֤��PB����O�����ߣ�
(2)��֪PA��![]() ����ACB��60��������O�İ뾶��
����ACB��60��������O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
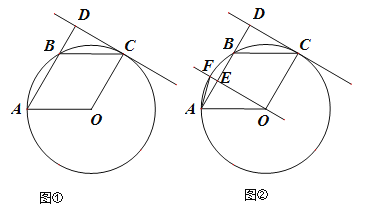
����Ŀ������С��10������֪A�� B��C����O�ϵ������㣬�ı���OABC��ƽ���ı��Σ�����C����O�����ߣ���AB���ӳ����ڵ�D��
��������ͼ��������ADC�Ĵ�С��
��������ͼ����������O��CD��ƽ���ߣ���AB���ڵ�E����![]() ���ڵ�F������AF������FAB�Ĵ�С��
���ڵ�F������AF������FAB�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC������Բ��O����ֱ�DZ�AB��BC�ֱ������ڵ�D��E�����ӻ�DE(�������˵�D��E)����һ��P����O������MN����AB��BC�ֱ��ڵ�M��N������O�İ뾶Ϊr����Rt��MBN���ܳ�Ϊ(����)
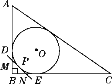
A. r B. ![]() r C. 2r D.
r C. 2r D. ![]() r
r
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
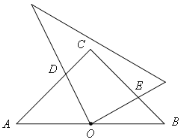
����Ŀ����ͼ,�ڵ���ֱ����ABC��,��C=90��,��O��AB���е�,��AB=![]() cm,��һ��ֱ�����ǰ��ֱ�Ƕ�����ڵ�O����ת,ʼ�ձ��ָ�ֱ�����ǰ����ֱ�DZ߷ֱ���AC��BC�ཻ,����ֱ�ΪD��E,��CD+CE=______cm.
cm,��һ��ֱ�����ǰ��ֱ�Ƕ�����ڵ�O����ת,ʼ�ձ��ָ�ֱ�����ǰ����ֱ�DZ߷ֱ���AC��BC�ཻ,����ֱ�ΪD��E,��CD+CE=______cm.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ƽ���ı���ABCD�У�E��F�ֱ�Ϊ��AB��CD���е㣬BD�ǶԽ��ߣ�AG��DB��CB���ӳ�����G��

��1����֤����ADE�ա�CBF��
��2�����ı��� BEDF�����Σ����ı���AGBD��ʲô�����ı��Σ���֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com