
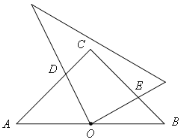
【题目】如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=![]() cm,将一块直角三角板的直角顶点放在点O处旋转,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE=______cm.
cm,将一块直角三角板的直角顶点放在点O处旋转,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE=______cm.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
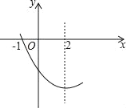
【题目】抛物线y=ax2+bx+c(a≠0)图象的一部分如图所示,其对称轴为x=2,与x轴的一个交点是(﹣1,0),有以下结论:①abc>0;②4a﹣2b+c<0;③4a+b=0④抛物线与x轴的另一个交点是(5,0)⑤若点(﹣3,y1)(﹣6,y2)都在抛物线上,则y1<y2.其中正确的是_____.(只填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
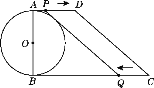
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=12 cm,AD=8 cm,BC=22 cm,AB为⊙O的直径,动点P从点A开始沿AD边向点D以1 cm/s的速度运动,动点Q从点C开始沿CB边向点B以2 cm/s的速度运动,P,Q分别从点A,C同时出发.当其中一动点到达终点时,另一个动点也随之停止运动.设运动时间为t s.当t为何值时,PQ与⊙O相切?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林准备进行如下操作实验:把一根长为40cm的铁丝剪成两段,并把每一段各围成一个正方形.
(1)要使这两个正方形的面积之和等于58cm2,小林该怎么剪?(求出剪成的两段铁丝的长度)
(2)小峰对小林说:“这两个正方形的面积之和不可能等于48cm2.”他的说法对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与函数y=![]() (x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=
(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=![]() OC,且△ACD的面积是6,连接BC.
OC,且△ACD的面积是6,连接BC.
(1)求m,k,n的值;
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
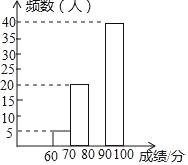
【题目】某校组织了一次全校2000名学生参加的比赛,赛后发现所有参赛学生的成绩均不低于60分,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(成绩x取整数,满分100分)作为样本进行整理,得到下列不完整的统计表:
请依据所给信息,解答下列问题:
(1)直接填空:a= ,b= ,c= ;
(2)请补全频数分布直方图;
(3)请自己提出一个与该题信息相关的问题,并解答你提出的问题.
成绩x/分 | 频数 | 频率 |
60≤x<70 | 5 | 0.05 |
70≤x<80 | 20 | b |
80≤x<90 | a | c |
90≤x≤100 | 40 | 0.40 |
查看答案和解析>>
科目:初中数学 来源: 题型:
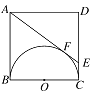
【题目】如图,正方形ABCD的边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MAN=30°,O为边AN上一点,以点O为圆心,2为半径作⊙O,交AN于D,E两点,设AD=x.
(1)如图①,当x取何值时,⊙O与AM相切?
(2)如图②,当x为何值时,⊙O与AM相交于B,C两点,且∠BOC=90°?
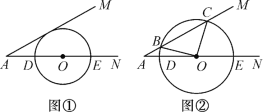
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com