
【题目】M是正方形ABCD的边AB上一动点(不与A,B重合),BP⊥MC,垂足为P,将∠CPB绕点P旋转,得到∠C’PB’,当射线PC’经过点D时,射线PB’与BC交于点N.
(1)依题意补全图形;
(2)求证:△BPN∽△CPD;
(3)在点M的运动过程中,图中是否存在与BM始终保持相等的线段?若存在,请写出这条线段并证明;若不存在,请说明理由.
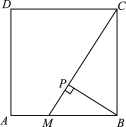
【答案】(1)见解析;(2)见解析;(3)BM=BN.
【解析】
(1)根据题意补全图形即可;
(2)由旋转性质知∠BPN=∠CPD,再由∠PCD+∠BCP=∠PBN+∠BCP=90°知∠PCD=∠PBN,从而得证;
(3)先证△MPB∽△BPC得![]() ,再由△PBN∽△PCD知
,再由△PBN∽△PCD知![]() ,从而得
,从而得![]() ,根据BC=CD可得答案.
,根据BC=CD可得答案.
(1)补全图形如图所示;
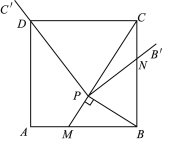
(2)证明:由旋转可得∠BPN=∠CPD.
∵四边形ABCD是正方形,
∴∠BCD=90°.
∴∠PCD+∠BCP=90°.
∵BP⊥MC,
∴∠CPB=90°.
∴∠PBC+∠PCB=90°.
∴∠PBC=∠PCD.
∴△PBN∽△PCD.
(3)答:BM=BN.
证明:∵BP⊥CM,∠MBC=90°,
∴∠MBP=∠MCB.
∴△MPB∽△BPC.
∴![]() .
.
由(2)可知△PBN∽△PCD.
∴![]() .
.
∴![]() .
.
∵BC=CD,
∴BM=BN.


科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示.
x | … | -3 | -2 | -1 | 0 | 1 | … |
y | … | -12 | -2 | 4 | 6 | 4 | … |
给出下列说法:①抛物线与y轴的交点为(0,6);②抛物线的对称轴是在y轴的右侧;③抛物线一定经过点(3,0);④当x<0时,函数值y随x的增大而减小.
从表中可知,上述说法正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2![]() cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形.
(2)若AB=5,AC=6,求四边形CODE的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场有一个可以自由转动的圆形转盘(如图).规定:顾客购物100元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品(指针指向两个扇形的交线时,当作指向右边的扇形).下表是活动进行中的一组统计数据:
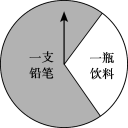
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 546 | 701 |
落在“铅笔”的频率 (结果保留小数点后两位) | 0.68 | 0.74 | 0.68 | 0.69 | 0.68 | 0.70 |
(1)转动该转盘一次,获得铅笔的概率约为_______;(结果保留小数点后一位)
(2)铅笔每只0.5元,饮料每瓶3元,经统计该商场每天约有4000名顾客参加抽奖活动,请计算该商场每天需要支出的奖品费用;
(3)在(2)的条件下,该商场想把每天支出的奖品费用控制在3000元左右,则转盘上“一瓶饮料”区域的圆心角应调整为______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市为方便行人过马路,打算修建一座高为4x(m)的过街天桥.已知天桥的斜面坡度i=1:0.75是指坡面的铅直高度DE(CF)与水平宽度AE(BF)的比,其中DC∥AB,CD=8x(m).
(1)请求出天桥总长和马路宽度AB的比;
(2)若某人从A地出发,横过马路直行(A→E→F→B)到达B地,平均速度是2.5m/s;返回时从天桥由BC→CD→DA到达A地,平均速度是1.5m/s,结果比去时多用了12.8s,请求出马路宽度AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,按照下列操作作图:①以A为圆心,AC长为半径画弧交AD的延长线于点E;②以E为圆心,EC长为半径画弧交DE的延长线于点F;③分别以C,F为圆心,大于![]() CF的长为半径画弧,两弧相交于点N;④作射线EN,根据作图,若∠ACB=72°,则∠FEN的度数为( )
CF的长为半径画弧,两弧相交于点N;④作射线EN,根据作图,若∠ACB=72°,则∠FEN的度数为( )
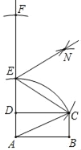
A. 54° B. 63° C. 72° D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=![]() cm.
cm.
(1)求证:AC是⊙O的切线;
(2)求由弦CD、BD与弧BC所围成的阴影部分的面积.(结果保留π)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com