
【题目】如图,抛物线与x轴交于点A(﹣![]() , 0),点B(2,0),与y轴交于点C(0,1),连接BC.
, 0),点B(2,0),与y轴交于点C(0,1),连接BC.
(1)求抛物线的解析式;
(2)N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t(﹣![]() ),求△ABN的面积s与t的函数解析式;
),求△ABN的面积s与t的函数解析式;
(3)若0<t<2且t≠0时,△OPN∽△COB,求点N的坐标.
【答案】解:(1)设抛物线的解析式为y=ax2+bx+c,由题意可得: ,
,
解得: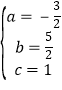 .
.
∴抛物线的函数关系式为y=﹣![]() x2+
x2+![]() x+1;
x+1;
(2)当﹣![]() <t<2时,yN>0,
<t<2时,yN>0,
∴NP=|yN|=yN=﹣![]() t2+
t2+![]() t+1,
t+1,
∴S=![]() ABPN
ABPN
=![]() ×(2+
×(2+![]() )×(﹣
)×(﹣![]() t2+
t2+![]() t+1)
t+1)
=![]() (﹣
(﹣![]() t2+
t2+![]() t+1)
t+1)
=﹣![]() t2+
t2+![]() t+
t+![]() ;
;
(3)∵△OPN∽△COB,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴PN=2PO.
当0<t<2时,PN=|yN|=yN=﹣![]() t2+
t2+![]() t+1,PO=|t|=t,
t+1,PO=|t|=t,
∴﹣![]() t2+
t2+![]() t+1=2t,
t+1=2t,
整理得:3t2﹣t﹣2=0,
解得:t3=﹣![]() ,t4=1.
,t4=1.
∵﹣![]() <0,0<1<2,
<0,0<1<2,
∴t=1,此时点N的坐标为(1,2).
故点N的坐标为(1,2).
【解析】(1)可设抛物线的解析式为y=ax2+bx+c,然后只需运用待定系数法就可解决问题;
(2)当﹣![]() <t<2时,点N在x轴的上方,则NP等于点N的纵坐标,只需求出AB,就可得到S与t的函数关系式;
<t<2时,点N在x轴的上方,则NP等于点N的纵坐标,只需求出AB,就可得到S与t的函数关系式;
(3)根据相似三角形的性质可得PN=2PO.由于PO=|t|,根据0<t<2,由PN=2PO得到关于t的方程,解这个方程,就可解决问题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,网格中每个小正方形的顶点叫格点,△OAB的顶点的坐标分别为O(0,0)、A(1,3)、B(5,0).
(1)请画出与△OAB关于原点对称的△OCD;(其中A的对称点为C,B的对称点为D)
(2)在(1)的条件下,连接BC、DA,请画出一条直线MN(不与直线AC和坐标轴重合),将四边形ABCD的面积分成相等的两部分,其中M、N分别在AD和BC上,且M、N均为格点,并直接写出直线MN的解析式(写出一个即可).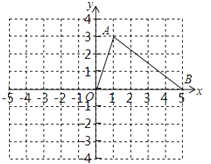
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数x,y在数轴上对应点如图所示:
![]()
(1)在数轴上表示﹣x,|y|;
(2)试把x,y,0,﹣x,|y|这五个数从小到大用“<”号连接,
(3)化简:|x+y|﹣|y﹣x|+|y|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强电动自行车质量监管,切实保障消费者的合法权益,2015年11月,河南开封市工商局对24个品牌批次的电动自行车进行抽查检验,其中抽查检验的某品牌的电动自行车如图所示,它的大灯M射出的光线MA,MB的与MN的夹角分别为76°和60°,MN⊥地面CD,MN=0.8m,图中的阴影部分表示在夜晚时,灯M所照射的范围.(提示:![]() ≈1.7,sin14°
≈1.7,sin14°![]() , cos14°≈
, cos14°≈![]() , tan14
, tan14![]() )
)
(1)求阴影部分的面积;
(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2s.小鹏某天晚上以6m/s的速度驾驶该车,在行驶的途中,通过大灯M,他发现在他的正前方有一个小球(即小孩在图中的点A处),小鹏从做出刹车动作到电动自行车停止的刹车距离为1.3m,请判断小鹏当时是否有撞到该小孩?(大灯M与前轮前端间的水平距离为0.3m).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平行四边形ABCD中,连接BD,AD=6cm,BD=8cm,∠DBC=90°,现将△AEF沿BD的方向匀速平移,速度为2cm/s,同时,点G从点D出发,沿DC的方向匀速移动,速度为2cm/s.当△AEF停止移动时,点G也停止运动,连接AD,AG,EG,过点E作EH⊥CD于点H,如图2所示,设△AEF的移动时间为t(s)(0<t<4).
(1)当t=1时,求EH的长度;
(2)若EG⊥AG,求证:EG2=AEHG;
(3)设△AGD的面积为y(cm2),当t为何值时,y可取得最大值,并求y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
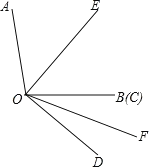
【题目】已知∠AOB=100°,∠COD=40°,OE平分∠AOC,OF平分∠BOD.(本题中的角均为大于0°且小于等于180°的角).
(1)如图1,当OB、OC重合时,求∠EOF的度数;
(2)当∠COD从图1所示位置绕点O顺时针旋转n°(0<n<90)时,∠AOE﹣∠BOF的值是否为定值?若是定值,求出∠AOE﹣∠BOF的值;若不是,请说明理由.
(3)当∠COD从图1所示位置绕点O顺时针旋转n°(0<n<180)时,满足∠AOD+∠EOF=6∠COD,则n=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.
(1)求证:∠DAC=∠DCE;
(2)若AB=2,sin∠D=![]() , 求AE的长.
, 求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径.PC是⊙O的切线,C为切点,PD⊥AB于点D,交AC于点E.
(1)求证:∠PCE=∠PEC;
(2)若AB=10,ED=![]() , sinA=
, sinA=![]() , 求PC的长.
, 求PC的长.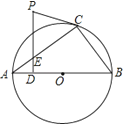
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com