Question

【题目】如图，在△ABC中，AB=BC，D是AC中点，BE平分∠ABD交AC于点E，点O是AB上一点，⊙O过B、E两点，交BD于点G，交AB于点F．

（1）判断直线AC与⊙O的位置关系，并说明理由；
（2）当BD=6，AB=10时，求⊙O的半径．

Answer 1

【答案】
（1）解：AC与⊙O相切．理由如下：

连结OE，如图，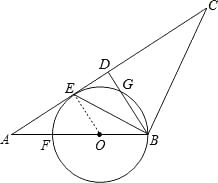

∵BE平分∠ABD，

∴∠OBE=∠DBO，

∵OE=OB，

∴∠OBE=∠OEB，

∴∠OBE=∠DBO，

∴OE∥BD，

∵AB=BC，D是AC中点，

∴BD⊥AC，

∴OE⊥AC，

∴AC与⊙O相切；

（2）解：设⊙O半径为r，则AO=10﹣r，

由（1）知，OE∥BD，

∴△AOE∽△ABD，

∴ ，即 ，

∴r= ，

即⊙O半径是 ．

【解析】（1）根据等腰三角形的性质，得到对边对等角，由角平分线的定义得到内错角相等，得到OE∥BD，根据等腰三角形的三线合一得到BD⊥AC，得到AC与⊙O相切；（2）根据（1）知，OE∥BD，得到△AOE∽△ABD，得到比例，求出⊙O的半径.
【考点精析】本题主要考查了切线的判定定理和相似三角形的判定与性质的相关知识点，需要掌握切线的判定方法：经过半径外端并且垂直于这条半径的直线是圆的切线；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方才能正确解答此题．