
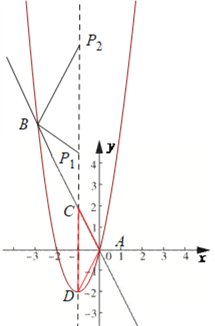
【题目】已知:如图,一次函数y=-2x与二次函数y=ax2+2ax+c的图像交于A、B两点(点A在点B的右侧),与其对称轴交于点C.
(1)求点C的坐标;
(2)设二次函数图像的顶点为D,点C与点D 关于 x轴对称,且△ACD的面积等于2.
① 求二次函数的解析式;
② 在该二次函数图像的对称轴上求一点P(写出其坐标),使△PBC与△ACD相似.
【答案】(1)C点的坐标为(-1,2);(2)①y=2x2+4x;②点P的坐标为(-1, 10),(-1, ![]() ).
).
【解析】试题分析:
(1)把y=ax2+2ax+c配方可得抛物线的对称轴为直线x=1,由此结合已知条件即可求得点C的坐标为(-1,2);
(2)①由(1)中的结论结合题意可得点D的坐标为(-1,-2),由此可得CD=4,结合△ACD的面积为2可得点A到CD的距离为1,结合点A是抛物线与直线y=-2x的交点可得点A与原点重合,即点A的坐标为(0,0),这样设抛物线的解析式为y-a(x+1)2-2,再代入点A的坐标即可求得a的值,从而可得抛物线的解析式;
②如下图,由已得抛物线的解析式结合题意可求得点B的坐标,再求结合点A、C、D的坐标即可得到AC、BC、CD的长,然后分△P1BC∽△ACD和△P1BC∽△ACD两种情况列出比例式,解出对应的P1C和P2C即可得到对应的点P的坐标了.
试题解析:
(1)∵y=ax2+2ax+c=a(x+1)2+c-a,
∴它的对称轴为x=-1.
又∵一次函数y=-2x与对称轴交于点C,
∴y=2,
∴C点的坐标为(-1,2).
(2)①∵点C与点D 关于x轴对称,
∴点D的坐标为(-1,-2).
∴CD=4,
∵△ACD的面积等于2.
∴点A到CD的距离为1,点A是抛物线与直线y=-2x的交点,
∴可得A点与原点重合,点A的坐标为(0,0),
设二次函数为y=a(x+1)2-2,∵其图象过点A(0,0),
∴a(0+1)2-2=0,解得a=2,
∴二次函数的解析式为:y=2x2+4x;
② 由![]() 解得:
解得: ![]() ,
, ![]() ,
,
∴点B的坐标为(-3,6),
∵点A、B、C、D的坐标分别为(0,0),(-3,6),(-1,2),D(-1,-2),
∴易得△ACD是等腰三角形,CD=4,AC=![]() ,BC=
,BC=![]() ,
,
如下图,①当△P2BC∽△CAD时,
![]() ,即
,即![]() ,解得P2C=8,
,解得P2C=8,
∴点P2到x轴的距离为10,即点P2的坐标为(-1,10);
②当△P1BC∽△ACD时,
![]() ,即
,即![]() ,解得P1C=2.5,
,解得P1C=2.5,
∴点P1到x轴的距离为4.5,即点P1的坐标为![]() .
.
∴综上所述可得:点P的坐标为(-1, 10),(-1, ![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表.
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |
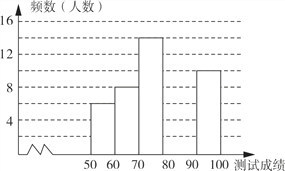
请结合图表完成下列各题:
(1)① 表中a的值为 ;
② 把频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小华两名射箭运动员在赛前的某次测试中射箭10次,成绩及各统计图如下图、表所示:
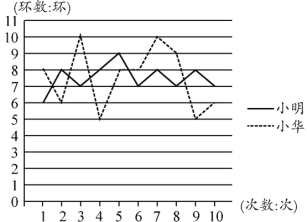
若让你选择其中一名参加比赛则你选择的运动员是:__________,理由是:_________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下(x>9且x<26,单位:km)
第一次 | 第二次 | 第三次 | 第四次 |
x |
| x﹣5 | 2(9﹣x) |
(1)说出这辆出租车每次行驶的方向.
(2)求经过连续4次行驶后,这辆出租车所在的位置.
(3)这辆出租车一共行驶了多少路程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“汉字听写大赛”活动,为了解学生的参与情况,在该校随机抽取了四个班级学生进行调查,将收集的数据整理并绘制成图1和图2两幅尚不完整的统计图,请根据图中的信息,解答下列问题:
(1)这四个班参与大赛的学生共__________人;
(2)请你补全两幅统计图;
(3)求图1中甲班所对应的扇形圆心角的度数;
(4)若四个班级的学生总数是160人,全校共2000人,请你估计全校的学生中参与这次活动的大约有多少人.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,从点O发出四条射线OA,OB,OC,OD,已知∠AOC=∠BOD=90°.
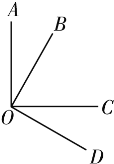
(1)若∠BOC=35°,则∠AOB= ,∠COD= ;
(2)若∠BOC=46°,则∠AOB= ,∠COD= .
(3)你发现了什么?你能说明其中的道理吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com