
【题目】如图所示,从点O发出四条射线OA,OB,OC,OD,已知∠AOC=∠BOD=90°.
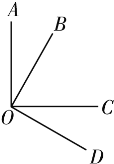
(1)若∠BOC=35°,则∠AOB= ,∠COD= ;
(2)若∠BOC=46°,则∠AOB= ,∠COD= .
(3)你发现了什么?你能说明其中的道理吗?
【答案】(1)∠AOB=55°,∠COD=55°.(2)∠AOB=44°,∠COD=44°. (3)∠AOB=∠COD
【解析】
(1)、(2)根据余角和补角的定义可直接得出结论;(3)根据(1)、(2)的计算及等式的性质可得出结论.
解:(1)∵∠AOC=∠BOD=90°.
∴∠AOB=90°-∠BOC=55°,∠COD=90°-∠BOC=55°.
(2) ∵∠AOC=∠BOD=90°.
∴∠AOB=90°-∠BOC=44°,∠COD=90°-∠BOC=44°.
(3)∠AOB=∠COD,
因为∠AOB+∠BOC=90°,∠COD+∠BOC=90°,
又因为∠BOC=∠BOC,
所以∠AOB=∠COD.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
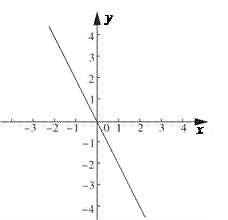
【题目】已知:如图,一次函数y=-2x与二次函数y=ax2+2ax+c的图像交于A、B两点(点A在点B的右侧),与其对称轴交于点C.
(1)求点C的坐标;
(2)设二次函数图像的顶点为D,点C与点D 关于 x轴对称,且△ACD的面积等于2.
① 求二次函数的解析式;
② 在该二次函数图像的对称轴上求一点P(写出其坐标),使△PBC与△ACD相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,图(1)为一个长方体,AD=AB=10,AE=6,图2为图1的表面展开图![]() 字在外表面上
字在外表面上![]() ,请根据要求回答问题:
,请根据要求回答问题:
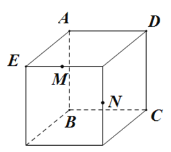

(1)面“句 ”的对面是面______;
(2)如果面“居”是右面,面“宜”在后面,哪一面会在上面?
(3)图(1)中,M、N为所在棱的中点,试在图(2)中画出点M、N的位置;并求出图(2)中三角形ABM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在桌面上,有若干个完全相同的小正方体堆成的一个几何体![]() ,如图所示.
,如图所示.

(1)请画出这个几何体![]() 的三视图.
的三视图.
(2)若将此几何体![]() 的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有_______个.
的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有_______个.
(3)若现在你的手头还有一些相同的小正方体可添放在几何体![]() 上,要保持主视图和左视图不变,则最多可以添加________个小正方体.
上,要保持主视图和左视图不变,则最多可以添加________个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
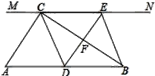
【题目】如图,在 Rt △ ABC 中,∠ ACB = 90 °,过点 C 的直线 MN ∥ AB , D 为 AB 边上一点,过点 D 作 DE ⊥ BC ,交直线 MN 于 E ,垂足为 F ,连接 CD 、 BE .(1)求证: CE = AD ;(2)当 D 在 AB 中点时,四边形 BECD 是什么特殊四边形?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学完“有理数的运算”后,我市某中学七年级每班各选出5名学生组成一个代表队,在数学老师的组织下进行一次知识竞赛.竞赛规则是:每队都必须回答50道题,答对一题得4分,不答或答错一题倒扣1分.
(1)如果七年级一班代表队最后得分为190分,那么七年级一班代表队回答对了多少道题?
(2)七年级二班代表队的最后得分有可能为142分吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,剪两张对边平行且宽度相同的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )
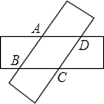
A. ∠ABC=∠ADC,∠BAD=∠BCDB. AB=BC
C. AB=CD,AD=BCD. ∠DAB+∠BCD=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,△ABC中,![]() ,AB的垂直平分线交AC于点D,连接BD.若AC=2,BC=1,则△BCD的周长为 ;
,AB的垂直平分线交AC于点D,连接BD.若AC=2,BC=1,则△BCD的周长为 ;
(2)O为正方形ABCD的中心,E为CD边上一点,F为AD边上一点,且△EDF的周长等于AD的长.
①在图2中求作△EDF(要求:尺规作图,不写作法,保留作图痕迹);
②在图3中补全图形,求![]() 的度数;
的度数;
③若![]() ,则
,则![]() 的值为 .
的值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在数轴上 A,B 两点对应数分别为﹣4,20.
(1)若 P 点为线段 AB 的中点,求 P 点对应的数.
(2)若点 A、点 B 同时分别以 2 个单位长度/秒的速度相向运动,点 M(M 点在原点)同时以 4 个单位长度/秒的速度向右运动.几秒后点 M 到点 A、点 B 的距离相等?求此时 M 对应的数.
(3)在(2)的条件下,是否存在 M 点,使 3MA=2MB?若存在,求出点 M 对应的数;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com