
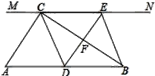
【题目】如图,在 Rt △ ABC 中,∠ ACB = 90 °,过点 C 的直线 MN ∥ AB , D 为 AB 边上一点,过点 D 作 DE ⊥ BC ,交直线 MN 于 E ,垂足为 F ,连接 CD 、 BE .(1)求证: CE = AD ;(2)当 D 在 AB 中点时,四边形 BECD 是什么特殊四边形?说明你的理由.
【答案】(1)见解析;(2)四边形 BECD 是菱形,理由见解析.
【解析】
(1)利用平行四边形对边平行可解答.
(2)利用证明菱形的条件即可解答.
证明:∵ DE ⊥ BC ,
∴∠ DFB = 90 °,
∵∠ ACB = 90 °,
∴∠ ACB =∠ DFB ,
∴ AC ∥ DE ,
∵ MN ∥ A B ,即 CE ∥ AD ,
∴四边形 ADEC 是平行四边形,
∴ CE = AD ;
( 2 )解:四边形 BECD 是菱形,理由如下:
∵ D 为 AB 中点,
∴ AD = BD ,
∵ CE = AD ,
∴ BD = CE ,
∵ BD ∥ CE ,
∴四边形 BECD 是平行四边形,
∵∠ ACB = 90 °, D 为 AB 中点,
∴ CD = BD ,
∴四边形 BECD 是菱形.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表.
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |
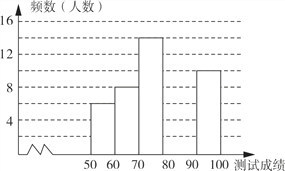
请结合图表完成下列各题:
(1)① 表中a的值为 ;
② 把频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为﹣3,B是数轴上位于点A右侧一点,且AB=12.动点P从点A出发,以每秒2个单位长度的速度沿数轴向点B方向匀速运动,设运动时间为t秒.
(1)数轴上点B表示的数为 ;点P表示的数为 (用含t的代数式表示).
(2)动点Q从点B出发,以每秒1个单位长度的速度沿数轴向点A方向匀速运动;点P、点Q同时出发,当点P与点Q重合后,点P马上改变方向,与点Q继续向点A方向匀速运动(点P、点Q在运动过程中,速度始终保持不变);当点P返回到达A点时,P、Q停止运动.设运动时间为t秒.
①当点P返回到达A点时,求t的值,并求出此时点Q表示的数.
②当点P是线段AQ的三等分点时,求t的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
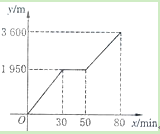
【题目】小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍.小颖在小亮出发后50min 才乘上缆车,缆车的平均速度为180m/min.设小亮出发x min后行走的路程为y m,图中 的折线表示小亮在整个行走过程中y与x的函数关系.
(1)小亮行走的总路程是___________m,他途中休息了_____________min;
(2)①当50<x<80时,求y与x的函数关系式;②当小颖到达缆车终点时,小亮离缆车终点的路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着出行方式的多样化,某地区打车有三种乘车方式,收费标准如下(假设打车的平均车速为30千米/小时):
网约出租车 | 网约顺风车 | 网约专车 |
3千米以内:12元 | 1.5元/千米 | 2元/千米 |
超过3千米的部分:2.4元/千米 | 0.5元/分钟 | 0.6元/分钟 |
(如:乘坐6千米,耗时12分钟,网约出租车的收费为:12+2.4×(6-3)=19.2(元);网约顺风车的收费为:6×1.5+12×0.5=15(元);网约专车的收费为:6×2+12×0.6=19.2(元))
请据此信息解决如下问题:
(1)王老师乘车从纵棹园去汽车站,全程8千米,如果王老师乘坐网约出租车,需要支付的打车费用为______元;
(2)李校长乘车从纵掉园去生态园,乘坐网约顺风车比乘坐网约出租车节省了2元.求从纵棹园去生态园的路程;
(3)网约专车为了和网约顺风车竞争客户,分别推出了优惠方式:网约顺风车对于乘车路程在5千米以上(含5千米)的客户每次收费立减6元;网约专车打车车费一律七五折优惠.对采用哪一种打车方式更合算提出你的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,从点O发出四条射线OA,OB,OC,OD,已知∠AOC=∠BOD=90°.
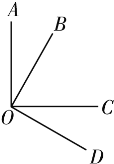
(1)若∠BOC=35°,则∠AOB= ,∠COD= ;
(2)若∠BOC=46°,则∠AOB= ,∠COD= .
(3)你发现了什么?你能说明其中的道理吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,
,![]() 试说明直线AD与BC垂直
试说明直线AD与BC垂直![]() 请在下面的解答过程的空格内填空或在括号内填写理由
请在下面的解答过程的空格内填空或在括号内填写理由![]() .
.
理由:![]() ,
,![]() 已知
已知![]()
![]() ______
______![]() ______,
______,![]() ______
______![]()
![]() ______
______![]() ______
______![]()
又![]() ,
,![]() 已知
已知![]()
![]() ______
______![]() 等量代换
等量代换![]()
![]() ______
______![]() ______,
______,![]() ______
______![]()
![]() ______
______![]()
![]() ,
,![]() 已知
已知![]()
![]() ,
,![]() ,
,
![]() ______
______![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
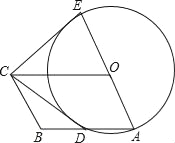
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若BC=4,CD=6,求平行四边形OABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
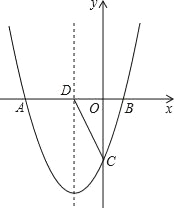
【题目】如图,抛物线y1=![]() 2+bx+c与x轴交于点A、B,交y轴于点C(0,﹣2
2+bx+c与x轴交于点A、B,交y轴于点C(0,﹣2![]() ),且抛物线对称轴x=﹣2交x轴于点D,E是抛物线在第3象限内一动点.
),且抛物线对称轴x=﹣2交x轴于点D,E是抛物线在第3象限内一动点.
(1)求抛物线y1的解析式;
(2)将△OCD沿CD翻折后,O点对称点O′是否在抛物线y1上?请说明理由.
(3)若点E关于直线CD的对称点E′恰好落在x轴上,过E′作x轴的垂线交抛物线y1于点F,①求点F的坐标;②直线CD上是否存在点P,使|PE﹣PF|最大?若存在,试写出|PE﹣PF|最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com