
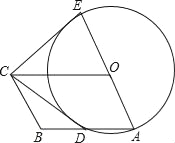
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若BC=4,CD=6,求平行四边形OABC的面积.
【答案】(1)证明见解析(2)24
【解析】试题分析:(1)连接OD,求出∠EOC=∠DOC,根据SAS推出△EOC≌△DOC,推出∠ODC=∠OEC=90°,根据切线的判定推出即可;
(2)根据切线长定理求出CE=CD=4,根据平行四边形性质求出OA=OD=4,根据平行四边形的面积公式=2△COD的面积即可求解.
试题解析:(1)证明:连接OD,
∵OD=OA,
∴∠ODA=∠A,
∵四边形OABC是平行四边形,
∴OC∥AB,
∴∠EOC=∠A,∠COD=∠ODA,
∴∠EOC=∠DOC,
在△EOC和△DOC中,
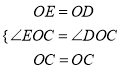
∴△EOC≌△DOC(SAS),
∴∠ODC=∠OEC=90°,
即OD⊥DC,
∴CD是⊙O的切线;
(2)由(1)知CD是圆O的切线,
∴△CDO为直角三角形,
∵S△CDO=![]() CDOD,
CDOD,
又∵OA=BC=OD=4,
∴S△CDO=![]() ×6×4=12,
×6×4=12,
∴平行四边形OABC的面积S=2S△CDO=24.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】已知![]()
(1)分别写出a,b,c表示的数,并计算(a+b)+(b+c)+(c+a)的值;
(2)设a,b,c在数轴上对应的点分别是点A,点B,点 C.若点M是线段AB上的一点,比较![]() 与MC的大小,说明理由.
与MC的大小,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
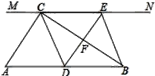
【题目】如图,在 Rt △ ABC 中,∠ ACB = 90 °,过点 C 的直线 MN ∥ AB , D 为 AB 边上一点,过点 D 作 DE ⊥ BC ,交直线 MN 于 E ,垂足为 F ,连接 CD 、 BE .(1)求证: CE = AD ;(2)当 D 在 AB 中点时,四边形 BECD 是什么特殊四边形?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,剪两张对边平行且宽度相同的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )
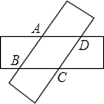
A. ∠ABC=∠ADC,∠BAD=∠BCDB. AB=BC
C. AB=CD,AD=BCD. ∠DAB+∠BCD=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中建立如图所示的平面直角坐标系xOy.△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:
(1)将△ABC向下平移5个单位长度,画出平移后的A1B1C1,并写出点A的对应点A1的坐标;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)将△ABC绕点C逆时针旋转90°,画出旋转后的△A3B3C.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,△ABC中,![]() ,AB的垂直平分线交AC于点D,连接BD.若AC=2,BC=1,则△BCD的周长为 ;
,AB的垂直平分线交AC于点D,连接BD.若AC=2,BC=1,则△BCD的周长为 ;
(2)O为正方形ABCD的中心,E为CD边上一点,F为AD边上一点,且△EDF的周长等于AD的长.
①在图2中求作△EDF(要求:尺规作图,不写作法,保留作图痕迹);
②在图3中补全图形,求![]() 的度数;
的度数;
③若![]() ,则
,则![]() 的值为 .
的值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会文艺部换届选举,经初选、复选后,共有 甲、乙、丙三人进入最后的竞选.最后决定利用投票方式对三人进行选举,共发出1800张选票,得票数最高者为当选人,且废票不计入任何一位候选人的得票数内,全校设有四个投票箱,目前第一、第二、第三投票箱已开完所有选票,剩下第四投票箱尚未开箱,结果如表所示(单位:票) 下列判断正确的是( )
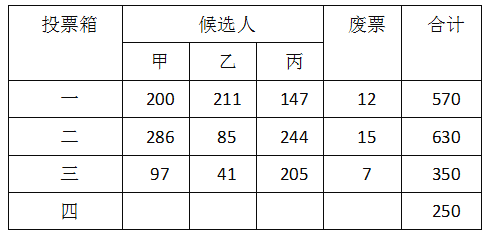
A. 甲可能当选 B. 乙可能当选 C. 丙一定当选 D. 甲、乙、丙三人都可能当选
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种计时“香篆”在0:00时刻点燃,若“香篆”剩余的长度h(cm)与燃烧的时间x(h)之间是一次函数关系,h与x的一组对应数值如表所示:
燃烧的时间x(h) | … | 3 | 4 | 5 | 6 | … |
剩余的长度h(cm) | … | 210 | 200 | 190 | 180 | … |
(1)写出“香篆”在0:00时刻点然后,其剩余的长度h(cm)与燃烧时间x(h)的函数关系式,并解释函数表达式中x的系数及常数项的实际意义;
(2)通过计算说明当“香篆”剩余的长度为125cm时的时刻.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ,
,![]() ,
,![]() ,垂足为
,垂足为![]() ,点
,点![]() 是边上
是边上![]() 的一个动点,连接
的一个动点,连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.

(1)请根据题意补全示意图;
(2)当![]() 与
与![]() 全等时,
全等时,
①若![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
②试探究![]() ,
,![]() ,
,![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com