
【题目】如图,在![]() ,
,![]() ,
,![]() ,垂足为
,垂足为![]() ,点
,点![]() 是边上
是边上![]() 的一个动点,连接
的一个动点,连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.

(1)请根据题意补全示意图;
(2)当![]() 与
与![]() 全等时,
全等时,
①若![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
②试探究![]() ,
,![]() ,
,![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
【答案】(1)见解析(2)①40°②![]() ,
,![]() ,
,![]() 之间的数量关系为:
之间的数量关系为:![]()
【解析】
(1)根据垂直画出图形即可得出结论;
(2)①先根据两三角形全等,判断出AB=DF,进而判断出BD=DE,再求出∠FDE=60°,进而利用三角形的外角的性质求出∠BDE=80°,进而求出∠DBE=∠BED=50°,即可得出结论;
②分两种情况:( I)若BD=DE,先判断出∠DBE=∠DEB=β,进而得出∠FBG=180°-α-β,进而得出∠FBG=∠DGE,再判断出FB=FG,即可得出结论;
( II)若AD=DE,先判断出DH>DE,再判断出∠A=∠BID,进而得出∠BID>∠C,即:∠A>∠C,即可判断出此种情况不成立.
解:(1)如图即为所求示意图.
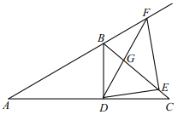
(2)①∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() 与
与![]() 全等,
全等,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
![]() .
.
在![]() 中,
中,![]()
∴![]() .
.
∵![]() ,
,
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 中,
中,
![]() .
.
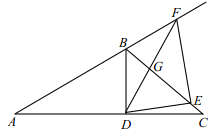
②![]() ,
,![]() ,
,![]() 之间的数量关系为:
之间的数量关系为:![]() .
.
证明:
由①得,![]() .
.
(Ⅰ)若![]() ,
,
设![]() ,
,![]() ,
,
∵![]() 与
与![]() 全等,
全等,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
在![]() 中,
中,![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
(Ⅱ)若![]() ,
,
如图,延长![]() 交
交![]() 于
于![]() ,
,
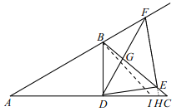
∵![]() ,
,
∴![]() .
.
则在线段![]() 上存在点
上存在点![]() ,使得
,使得![]() .
.
连接![]() ,
,
∵![]() ,
,
又∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
不符合题意.
综上所述,![]() ,
,![]() ,
,![]() 之间的数量关系为:
之间的数量关系为:![]() .
.


科目:初中数学 来源: 题型:
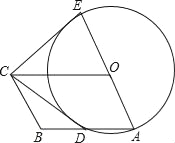
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若BC=4,CD=6,求平行四边形OABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
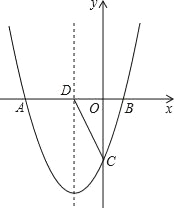
【题目】如图,抛物线y1=![]() 2+bx+c与x轴交于点A、B,交y轴于点C(0,﹣2
2+bx+c与x轴交于点A、B,交y轴于点C(0,﹣2![]() ),且抛物线对称轴x=﹣2交x轴于点D,E是抛物线在第3象限内一动点.
),且抛物线对称轴x=﹣2交x轴于点D,E是抛物线在第3象限内一动点.
(1)求抛物线y1的解析式;
(2)将△OCD沿CD翻折后,O点对称点O′是否在抛物线y1上?请说明理由.
(3)若点E关于直线CD的对称点E′恰好落在x轴上,过E′作x轴的垂线交抛物线y1于点F,①求点F的坐标;②直线CD上是否存在点P,使|PE﹣PF|最大?若存在,试写出|PE﹣PF|最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上线段AB=2(单位长度),线段CD=4(单位长度),点A在数轴上表示的数是-10,点C在数轴上表示的数是16.若线段AB以每秒6个单位长度的速度向右匀速运动,同时线段CD以每秒2个单位长度的速度向左匀速运动.设运动时间为t s.
(1)当点B与点C相遇时,点A、点D在数轴上表示的数分别为________;
(2)当t为何值时,点B刚好与线段CD的中点重合;
(3)当运动到BC=8(单位长度)时,求出此时点B在数轴上表示的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
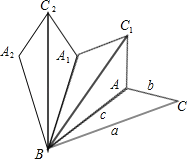
【题目】在△ABC中,∠ABC<20°,三边长分别为a,b,c,将△ABC沿直线BA翻折,得到△ABC1;然后将△ABC1沿直线BC1翻折,得到△A1BC1;再将△A1BC1沿直线A1B翻折,得到△A1BC2;…,若翻折4次后,得到图形A2BCAC1A1C2的周长为a+c+5b,则翻折11次后,所得图形的周长为_____________.(结果用含有a,b,c的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
![]()
若n=13,则第2018次“F”运算的结果是( )
A. 1 B. 4 C. 2018 D. 42018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某种电动汽车的性能,某机构对这种电动汽车进行抽检,获得如图中不完整的统计图,其中![]() ,
,![]() ,
,![]() ,
,![]() 表示 一次充电后行驶的里程数分别为
表示 一次充电后行驶的里程数分别为![]() ,
,![]() ,
,![]() ,
,![]() .
.
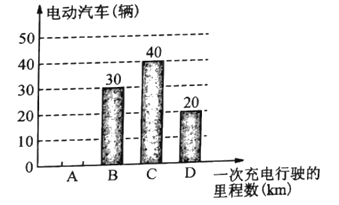
(1)问这次被抽检的电动汽车共有几辆?并补全条形统计图;
电动汽车一次充电后行驶里程数的条形统计图
电动汽车一次充电后行驶里程数的扇形统计图
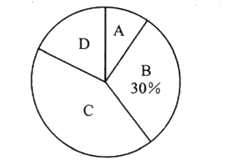
(2)求扇形统计图中表示一次充电后行驶路为![]() 的扇形圆心角的度数;
的扇形圆心角的度数;
(3)估计这种电动汽车一次充电后行驶的平均里程多少![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段AB=12cm,点C为线段AB上的一动点,点D,E分别是AC和BC中点.
(1)若点C恰好是AB的中点,则DE=_______cm;
(2)若AC=4cm,求DE的长;
(3)试说明无论AC取何值(不超过12cm),DE的长不变;
(4)如图②,已知∠AOB=120°,过角的内部任一点C画射线OC.若OD,OE分别平分∠AOC和∠BOC.试说明∠DOE的度数与射线OC的位置无关.
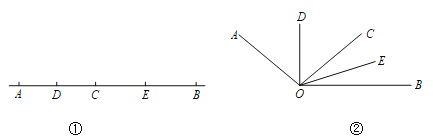
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探索新知)
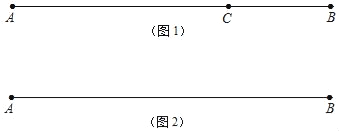
如图1,点C在线段AB上,图中共有3条线段:AB、AC和BC,若其中有一条线段的长度是另一条线段长度的两倍,则称点C是线段AB的“二倍点”.
(1)一条线段的中点 这条线段的“二倍点”;(填“是”或“不是”)
(深入研究)
如图2,若线段AB=20cm,点M从点B的位置开始,以每秒2cm的速度向点A运动,当点M到达点A时停止运动,运动的时间为t秒.
(2)问t为何值时,点M是线段AB的“二倍点”;
(3)同时点N从点A的位置开始,以每秒1cm的速度向点B运动,并与点M同时停止.请直接写出点M是线段AN的“二倍点”时t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com