
����Ŀ��Ϊ���˽�ij�ֵ綯���������ܣ�ij���������ֵ綯�������г�죬�����ͼ�в�������ͳ��ͼ������![]() ��
��![]() ��
��![]() ��
��![]() ��ʾ һ�γ�����ʻ��������ֱ�Ϊ
��ʾ һ�γ�����ʻ��������ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��![]() .
.
��1������α����ĵ綯�������м���������ȫ����ͳ��ͼ��
�綯����һ�γ�����ʻ�����������ͳ��ͼ
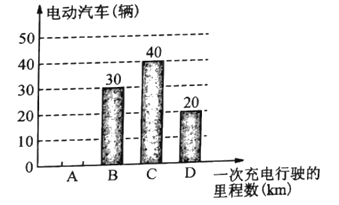
�綯����һ�γ�����ʻ�����������ͳ��ͼ
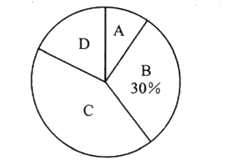
��2��������ͳ��ͼ�б�ʾһ�γ�����ʻ·Ϊ![]() ������Բ�ĽǵĶ�����
������Բ�ĽǵĶ�����
��3���������ֵ綯����һ�γ�����ʻ��ƽ����̶���![]() ��
��
���𰸡���1���ܹ���![]() ��.
��.![]() ����10����ͼ�ԣ���2��72�㣻��3�����ֵ綯����һ�γ�����ʻ��ƽ�������Ϊ
����10����ͼ�ԣ���2��72�㣻��3�����ֵ綯����һ�γ�����ʻ��ƽ�������Ϊ![]() ǧ��.
ǧ��.
��������
��1����������ͳ��ͼ������ͼ��֪����һ�γ�����ʻ���������ΪB�ȼ�����30���綯��������ռ�İٷֱ�Ϊ30%����30��30%���������α����ĵ綯�����������ٷֱ��ȥB��C��D�ȼ����������õ�A�ȼ������������ɲ�ȫ����ͼ��
��2����D�ȼ����������������������õ�����ռ�İٷֱȣ��ٳ���360���õ�����Բ�ĽǵĶ�����
��3��������̳������������������ɽ��
�⣺��1����α����ĵ綯��������30��30%=100��������
A�ȼ���������Ϊ��100-��30+40+20��=10��������
����ͼ�������£�

��2��D�ȼ���Ӧ��Բ�ĽǶ���Ϊ![]() .
.
��3��![]() .
.
�����ֵ綯����һ�γ�����ʻ��ƽ�������Ϊ![]() ǧ��.
ǧ��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУѧ�������ղ�����ѡ��������ѡ����ѡ�������� �ס��ҡ������˽������ľ�ѡ������������ͶƱ��ʽ�����˽���ѡ����������1800��ѡƱ����Ʊ�������Ϊ��ѡ�����ҷ�Ʊ�������κ�һλ��ѡ�˵ĵ�Ʊ������ȫУ�����ĸ�ͶƱ����Ŀǰ��һ���ڶ�������ͶƱ���ѿ�������ѡƱ��ʣ�µ���ͶƱ����δ��������������ʾ����λ��Ʊ�� �����ж���ȷ������ ��
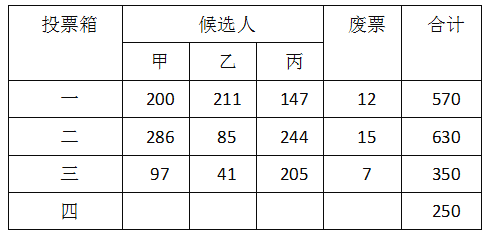
A. ���ܵ�ѡ B. �ҿ��ܵ�ѡ C. ��һ����ѡ D. �ס��ҡ������˶����ܵ�ѡ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
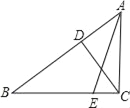
����Ŀ����֪���ڡ�ABC�У���ACB=90�㣬CD��AB��D��BE��AB=3��5����CE=![]() ��cos��ACD=
��cos��ACD=![]() ��
��
��1����cos��ABC��
��2��AC��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ��
��![]() ��
��![]() ������Ϊ
������Ϊ![]() ����
����![]() �DZ���
�DZ���![]() ��һ�����㣬����
��һ�����㣬����![]() ������
������![]() ��
��![]() ����
����![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() .
.

��1����������ⲹȫʾ��ͼ��
��2����![]() ��
��![]() ȫ��ʱ��
ȫ��ʱ��
����![]() ��
��![]() ��
��![]() ����
����![]() �Ķ�����
�Ķ�����
����̽��![]() ��
��![]() ��
��![]() ֮���������ϵ����֤��.
֮���������ϵ����֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ű���Ͱ͡��Ա�����������С�Ȼ�������ͷ�����𣬴����˿����ҵ�ĸ��ٷ�չ���ݵ��飬������ij��С�Ϳ�ݹ�˾������һ�·������·����Ͷ�ݵĿ���ܼ����ֱ�Ϊ10�����12.1������ּٶ��ù�˾ÿ��Ͷ�ݵĿ���ܼ�������������ͬ��
��1����ÿ�ݹ�˾Ͷ�ݿ���ܼ�������ƽ�������ʣ�
��2�����ƽ��ÿ��ÿ������Ͷ�ݿ��0.6�������ô�ù�˾���е�21�����Ͷ��ҵ��Ա�ܷ���ɽ���4�·ݵĿ��Ͷ������������ܣ�����������Ҫ���Ӽ���ҵ��Ա��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A=��xy��x��1,B=4x��3y,
��1����x=��2�� y=0.6ʱ����A+2B��ֵ��
��2��������ʽ2A��B�Ľ������ĸy��ȡֵ�أ���x��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�����
�������еĹ��ɣ��������еķ��������ϵ��µ����ֱ���_____��_____��
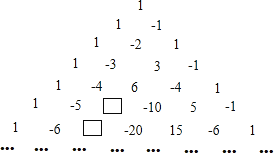
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y=��kx+k�뷴��������y=��![]() ��k��0����ͬһ����ϵ�е�ͼ������ǣ�������
��k��0����ͬһ����ϵ�е�ͼ������ǣ�������
A.  B.
B. 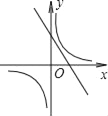 C.
C.  D.
D. 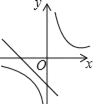
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90������ACΪֱ������O����AB��D������O��OE��AB����BC��E��
��1����֤��EDΪ��O�����ߣ�
��2�������O�İ뾶Ϊ![]() ��ED=2���ӳ�EO����O��F������DF��AF������ADF�������
��ED=2���ӳ�EO����O��F������DF��AF������ADF�������

���𰸡���1��֤������������2��![]()
�������������������1����������OD����OE��AB������ƽ��������������ε����ʣ���֤��![]() ��
��![]() ���ɵ�
���ɵ�![]() �����֤��
�����֤��![]() Ϊ
Ϊ![]() �����ߣ�
�����ߣ�
��2������CD������ֱ�����Ե�Բ�ܽ���ֱ�ǣ����ɵ�![]() ���ù��ɶ����������
���ù��ɶ����������![]() �ij�������OE��AB��֤��
�ij�������OE��AB��֤��![]() �������������εĶ�Ӧ�߳ɱ������������
�������������εĶ�Ӧ�߳ɱ������������![]() �ij���Ȼ���������Ǻ�����֪ʶ�����
�ij���Ȼ���������Ǻ�����֪ʶ�����![]() ��
��![]() �ij���Ȼ������S��ADF=S����ABEF-S����DBEF��ô𰸣�
�ij���Ȼ������S��ADF=S����ABEF-S����DBEF��ô𰸣�
���������(1)֤��������OD��

��OE��AB��
���COE=��CAD����EOD=��ODA��
��OA=OD,
���OAD=��ODA��
���COE=��DOE��
�ڡ�COE�͡�DOE�У�
 ���COE�ա�DOE(SAS)��
���COE�ա�DOE(SAS)��
![]()
��ED��OD��
��ED��![]() �����ߣ�
�����ߣ�
(2)����CD����OE��M��
��Rt��ODE��
��OD=32��DE=2��
![]()
��OE��AB��
���COE�ס�CAB��
![]() ��AB=5��
��AB=5��
��AC��ֱ����
![]()
![]()
![]()
![]()
��EF��AB��
![]()
![]()
![]()
��S��ADF=S����ABEFS����DBEF
![]()
���ADF�����Ϊ![]()

�����͡������
��������
25
����Ŀ������Ŀ����֪��������y=ax2+ax+b��a��0����ֱ��y=2x+m��һ��������M��1��0������a��b��
��1����b��a�Ĺ�ϵʽ�������ߵĶ���D���꣨��a�Ĵ���ʽ��ʾ����
��2��ֱ���������ߵ�����һ�������ΪN������DMN�������a�Ĺ�ϵʽ��
��3��a=��1ʱ��ֱ��y=��2x���������ڵڶ������ڵ�G����G��H����ԭ��Գƣ��ֽ��߶�GH��y������ƽ��t����λ��t��0�������߶�GH����������������ͬ�Ĺ����㣬����t��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com