
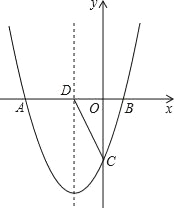
【题目】如图,抛物线y1=![]() 2+bx+c与x轴交于点A、B,交y轴于点C(0,﹣2
2+bx+c与x轴交于点A、B,交y轴于点C(0,﹣2![]() ),且抛物线对称轴x=﹣2交x轴于点D,E是抛物线在第3象限内一动点.
),且抛物线对称轴x=﹣2交x轴于点D,E是抛物线在第3象限内一动点.
(1)求抛物线y1的解析式;
(2)将△OCD沿CD翻折后,O点对称点O′是否在抛物线y1上?请说明理由.
(3)若点E关于直线CD的对称点E′恰好落在x轴上,过E′作x轴的垂线交抛物线y1于点F,①求点F的坐标;②直线CD上是否存在点P,使|PE﹣PF|最大?若存在,试写出|PE﹣PF|最大值.
【答案】(1)抛物线解析式为y1=![]() x2+2x﹣2
x2+2x﹣2![]() ;(2)O点对称点O′不在抛物线y1上,理由见解析;(3)①F(2,6﹣2
;(2)O点对称点O′不在抛物线y1上,理由见解析;(3)①F(2,6﹣2![]() );②直线CD上存在点P,使|PE﹣PF|最大,最大值为6﹣2
);②直线CD上存在点P,使|PE﹣PF|最大,最大值为6﹣2![]() .
.
【解析】试题分析:(1)先由抛物线对称轴方程可求出b=2,再把点C(0,﹣2![]() )代入y1=
)代入y1=![]() x2+bx+c可得c=2
x2+bx+c可得c=2![]() ,所以抛物线解析式为y1=
,所以抛物线解析式为y1=![]() x2+2x﹣2
x2+2x﹣2![]() ;
;
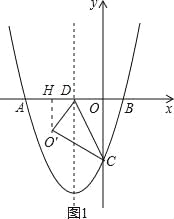
(2)过O′点作O′H⊥x轴于H,如图1,由(1)得D(﹣2,0),C(0,2![]() ),在Rt△OCD中利用三角函数可计算出∠ODC=60°,再利用折叠的性质得O′D=OD=2,∠O′DC=∠ODC=60°,所以∠O′DH=60°,接着在Rt△O′DH中利用三角函数可计算出O′H=
),在Rt△OCD中利用三角函数可计算出∠ODC=60°,再利用折叠的性质得O′D=OD=2,∠O′DC=∠ODC=60°,所以∠O′DH=60°,接着在Rt△O′DH中利用三角函数可计算出O′H=![]() ,利用勾股定理计算出DH=1,则O′(﹣3,﹣
,利用勾股定理计算出DH=1,则O′(﹣3,﹣![]() ),然后根据二次函数图象上点的坐标特征判断O′点是否在抛物线y1上;
),然后根据二次函数图象上点的坐标特征判断O′点是否在抛物线y1上;
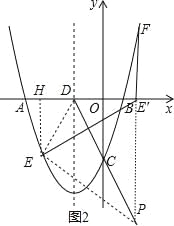
(3)①利用二次函数图象上点的坐标特征设E(m, ![]() m2+2m﹣2
m2+2m﹣2![]() )(m<0),过E作EH⊥x轴于H,连结DE,如图2,则DH=﹣2﹣m,EH=﹣
)(m<0),过E作EH⊥x轴于H,连结DE,如图2,则DH=﹣2﹣m,EH=﹣![]() m2﹣2m+2
m2﹣2m+2![]() ,由(2)得∠ODC=60°,再利用轴对称性质得DC平分∠EDE′,DE=DE′,则∠EDE′=120°,所以∠EDH=60°,于是在Rt△EDH中利用三角函数的定义可得﹣
,由(2)得∠ODC=60°,再利用轴对称性质得DC平分∠EDE′,DE=DE′,则∠EDE′=120°,所以∠EDH=60°,于是在Rt△EDH中利用三角函数的定义可得﹣![]() m2﹣2m+2
m2﹣2m+2![]() =(﹣2﹣m)
=(﹣2﹣m)![]() ,解得m1=2
,解得m1=2![]() (舍去),m2=﹣4,则E(﹣4,﹣2
(舍去),m2=﹣4,则E(﹣4,﹣2![]() ),接着计算出DE=4,所以DE′=4,于是得到E′(2,0),然后计算x=2时得函数值即可得到F点坐标;
),接着计算出DE=4,所以DE′=4,于是得到E′(2,0),然后计算x=2时得函数值即可得到F点坐标;
②由于点E关于直线CD的对称点E′恰好落在x轴,则PE=PE′,根据三角形三边的关系得|PE′﹣PF|≤E′F(当点P、E′F共线时,取等号),于是可判断直线CD上存在点P,使|PE﹣PF|最大,最大值为6﹣2![]() .
.
试题解析:(1)∵抛物线对称轴x=﹣2,
∴﹣![]() =﹣2,
=﹣2,
解得b=2,
∵点C(0,﹣2![]() )在抛物线y1=
)在抛物线y1=![]() x2+bx+c上,
x2+bx+c上,
∴c=2![]() ,
,
∴抛物线解析式为y1=![]() x2+2x﹣2
x2+2x﹣2![]() ;
;
(2)O点对称点O′不在抛物线y1上.理由如下:
过O′点作O′H⊥x轴于H,如图1,由(1)得D(﹣2,0),C(0,2![]() ),
),
在Rt△OCD中,∵OD=2,OC=![]() ,
,
∴tan∠ODC=![]() =
=![]() ,
,
∴∠ODC=60°,
∵△OCD沿CD翻折后,O点对称点O′,
∴O′D=OD=2,∠O′DC=∠ODC=60°,
∴∠O′DH=60°,
在Rt△O′DH中,sin∠O′DH=![]() ,
,
∴O′H=2sin60°=![]() ,
,
∴DH=![]() =1,
=1,
∴O′(﹣3,﹣![]() ),
),
∵当x=﹣3时,y1=![]() x2+2x﹣2
x2+2x﹣2![]() =
=![]() ×9+2×(﹣3)﹣2
×9+2×(﹣3)﹣2![]() ≠﹣
≠﹣![]() ,
,
∴O′点不在抛物线y1上;
(3)①设E(m, ![]() m2+2m﹣2
m2+2m﹣2![]() )(m<0),
)(m<0),
过E作EH⊥x轴于H,连结DE,如图2,则DH=﹣2﹣m,EH=﹣(![]() m2+2m﹣2
m2+2m﹣2![]() )=﹣
)=﹣![]() m2﹣2m+2
m2﹣2m+2![]() ,
,
由(2)得∠ODC=60°,
∵点E关于直线CD的对称点E′恰好落在x轴上,
∴DC垂直平分EE′,
∴DC平分∠EDE′,DE=DE′,
∴∠EDE′=120°,
∴∠EDH=60°,
在Rt△EDH中,∵tan∠EDH=![]() ,
,
∴EH=HDtan60°,即﹣![]() m2﹣2m+2
m2﹣2m+2![]() =(﹣2﹣m)
=(﹣2﹣m)![]() ,
,
整理得m2+(4+2![]() )m﹣8
)m﹣8![]() =0,解得m1=2
=0,解得m1=2![]() (舍去),m2=﹣4,
(舍去),m2=﹣4,
∴E(﹣4,﹣2![]() ),
),
∴HD=2,EH=2![]() ,
,
∴DE=![]() =4,
=4,
∴DE′=4,
∴E′(2,0),
而E′F⊥x轴,
∴F点的横坐标为2,
当x=2时,y1=![]() x2+2x﹣2
x2+2x﹣2![]() =6﹣2
=6﹣2![]() ,
,
∴F(2,6﹣2![]() );
);
②∵点E关于直线CD的对称点E′恰好落在x轴,
∴PE=PE′,
∴|PE′﹣PF|≤E′F(当点P、E′F共线时,取等号),
∴直线CD上存在点P,使|PE﹣PF|最大,最大值为6﹣2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
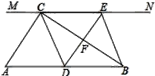
【题目】如图,在 Rt △ ABC 中,∠ ACB = 90 °,过点 C 的直线 MN ∥ AB , D 为 AB 边上一点,过点 D 作 DE ⊥ BC ,交直线 MN 于 E ,垂足为 F ,连接 CD 、 BE .(1)求证: CE = AD ;(2)当 D 在 AB 中点时,四边形 BECD 是什么特殊四边形?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会文艺部换届选举,经初选、复选后,共有 甲、乙、丙三人进入最后的竞选.最后决定利用投票方式对三人进行选举,共发出1800张选票,得票数最高者为当选人,且废票不计入任何一位候选人的得票数内,全校设有四个投票箱,目前第一、第二、第三投票箱已开完所有选票,剩下第四投票箱尚未开箱,结果如表所示(单位:票) 下列判断正确的是( )
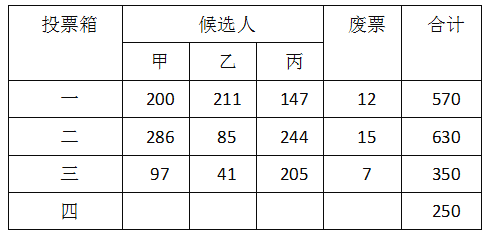
A. 甲可能当选 B. 乙可能当选 C. 丙一定当选 D. 甲、乙、丙三人都可能当选
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种计时“香篆”在0:00时刻点燃,若“香篆”剩余的长度h(cm)与燃烧的时间x(h)之间是一次函数关系,h与x的一组对应数值如表所示:
燃烧的时间x(h) | … | 3 | 4 | 5 | 6 | … |
剩余的长度h(cm) | … | 210 | 200 | 190 | 180 | … |
(1)写出“香篆”在0:00时刻点然后,其剩余的长度h(cm)与燃烧时间x(h)的函数关系式,并解释函数表达式中x的系数及常数项的实际意义;
(2)通过计算说明当“香篆”剩余的长度为125cm时的时刻.

查看答案和解析>>
科目:初中数学 来源: 题型:
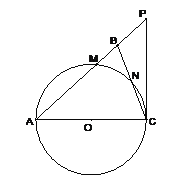
【题目】如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)求证:直线CP是⊙O的切线;
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求⊙O的半径及△ACP的周长.
,求⊙O的半径及△ACP的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在数轴上 A,B 两点对应数分别为﹣4,20.
(1)若 P 点为线段 AB 的中点,求 P 点对应的数.
(2)若点 A、点 B 同时分别以 2 个单位长度/秒的速度相向运动,点 M(M 点在原点)同时以 4 个单位长度/秒的速度向右运动.几秒后点 M 到点 A、点 B 的距离相等?求此时 M 对应的数.
(3)在(2)的条件下,是否存在 M 点,使 3MA=2MB?若存在,求出点 M 对应的数;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
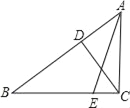
【题目】已知:在△ABC中,∠ACB=90°,CD⊥AB于D,BE:AB=3:5,若CE=![]() ,cos∠ACD=
,cos∠ACD=![]() .
.
(1)求cos∠ABC;
(2)AC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ,
,![]() ,
,![]() ,垂足为
,垂足为![]() ,点
,点![]() 是边上
是边上![]() 的一个动点,连接
的一个动点,连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.

(1)请根据题意补全示意图;
(2)当![]() 与
与![]() 全等时,
全等时,
①若![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
②试探究![]() ,
,![]() ,
,![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com