
【题目】某种计时“香篆”在0:00时刻点燃,若“香篆”剩余的长度h(cm)与燃烧的时间x(h)之间是一次函数关系,h与x的一组对应数值如表所示:
燃烧的时间x(h) | … | 3 | 4 | 5 | 6 | … |
剩余的长度h(cm) | … | 210 | 200 | 190 | 180 | … |
(1)写出“香篆”在0:00时刻点然后,其剩余的长度h(cm)与燃烧时间x(h)的函数关系式,并解释函数表达式中x的系数及常数项的实际意义;
(2)通过计算说明当“香篆”剩余的长度为125cm时的时刻.

【答案】(1)x的系数表示“香篆”每小时燃烧10cm,常数项表示“香篆”未点燃之前的长度为240cm;;(2)“香篆”在0:00点燃后,燃烧了11.5小时后的时刻为11点30分.
【解析】
(1)根据待定系数法确定函数关系式即可求解;
(2)把h=125代入解析式即可求解.
解:(1)∵“香篆”在0:00时刻点然后,其剩余的长度h(cm)与燃烧时间x(h)的函数关系式是一次函数,
设一次函数的解析式为:h=kx+b,
∵当x=3时,h=210,当x=4时,h=200,
可得:![]() ,
,
解得:![]() ,
,
所以解析式为:h=﹣10x+240,
x的系数表示“香篆”每小时燃烧10cm,常数项表示“香篆”未点燃之前的长度为240cm;
(2)当“香篆”剩余125cm时,可知h=125,代入解析式得:125=﹣10x+240,
解得:x=11.5,
所以“香篆”在0:00点燃后,燃烧了11.5小时后的时刻为11点30分.


科目:初中数学 来源: 题型:
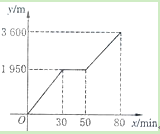
【题目】小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍.小颖在小亮出发后50min 才乘上缆车,缆车的平均速度为180m/min.设小亮出发x min后行走的路程为y m,图中 的折线表示小亮在整个行走过程中y与x的函数关系.
(1)小亮行走的总路程是___________m,他途中休息了_____________min;
(2)①当50<x<80时,求y与x的函数关系式;②当小颖到达缆车终点时,小亮离缆车终点的路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
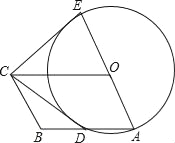
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若BC=4,CD=6,求平行四边形OABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点M,O,N对应的数分别为﹣2,0,4,点P为数轴上任意一点,其对应的数为x.
(1)如果点P到点M点N的距离相等,则x= .
(2)数轴上是否存在点P,使点P到点M、点N的距离之和是10?若存在,求出x的值;若不存在,请说明理由.
(3)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知y﹣2与x成正比例,且x=2时,y=﹣6.①求y与x之间的函数关系式;②当y<3时,求x的取值范围.
(2)已知经过点(﹣2,﹣2)的直线l1:y1=mx+n与直线l2:y2=﹣2x+6相交于点M(1,p)
①关于x,y的二元一次方程组![]() 的解为 ;②求直线l1的表达式.
的解为 ;②求直线l1的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
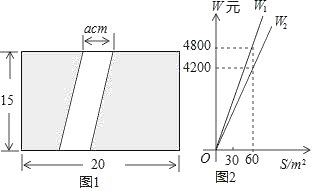
【题目】如图1,为美化校园环境,某校计划在一块长为20m,宽为15m的长方形空地上修建一条宽为a(m)的甬道,余下的部分铺设草坪建成绿地.
(1)甬道的面积为 m2,绿地的面积为 m2(用含a的代数式表示);
(2)已知某公园公司修建甬道,绿地的造价W1(元),W2(元)与修建面积S之间的函数关系如图2所示.①园林公司修建一平方米的甬道,绿地的造价分别为 元, 元.②直接写出修建甬道的造价W1(元),修建绿地的造价W2(元)与a(m)的关系式;③如果学校决定由该公司承建此项目,并要求修建的甬道宽度不少于2m且不超过5m,那么甬道宽为多少时,修建的甬道和绿地的总造价最低,最低总造价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
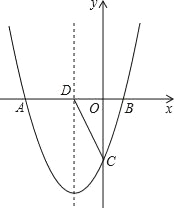
【题目】如图,抛物线y1=![]() 2+bx+c与x轴交于点A、B,交y轴于点C(0,﹣2
2+bx+c与x轴交于点A、B,交y轴于点C(0,﹣2![]() ),且抛物线对称轴x=﹣2交x轴于点D,E是抛物线在第3象限内一动点.
),且抛物线对称轴x=﹣2交x轴于点D,E是抛物线在第3象限内一动点.
(1)求抛物线y1的解析式;
(2)将△OCD沿CD翻折后,O点对称点O′是否在抛物线y1上?请说明理由.
(3)若点E关于直线CD的对称点E′恰好落在x轴上,过E′作x轴的垂线交抛物线y1于点F,①求点F的坐标;②直线CD上是否存在点P,使|PE﹣PF|最大?若存在,试写出|PE﹣PF|最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上线段AB=2(单位长度),线段CD=4(单位长度),点A在数轴上表示的数是-10,点C在数轴上表示的数是16.若线段AB以每秒6个单位长度的速度向右匀速运动,同时线段CD以每秒2个单位长度的速度向左匀速运动.设运动时间为t s.
(1)当点B与点C相遇时,点A、点D在数轴上表示的数分别为________;
(2)当t为何值时,点B刚好与线段CD的中点重合;
(3)当运动到BC=8(单位长度)时,求出此时点B在数轴上表示的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段AB=12cm,点C为线段AB上的一动点,点D,E分别是AC和BC中点.
(1)若点C恰好是AB的中点,则DE=_______cm;
(2)若AC=4cm,求DE的长;
(3)试说明无论AC取何值(不超过12cm),DE的长不变;
(4)如图②,已知∠AOB=120°,过角的内部任一点C画射线OC.若OD,OE分别平分∠AOC和∠BOC.试说明∠DOE的度数与射线OC的位置无关.
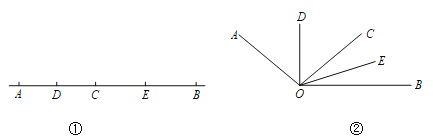
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com