
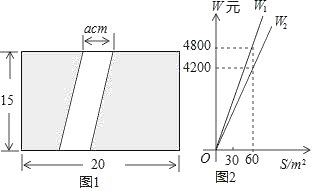
����Ŀ����ͼ1��Ϊ����У������ijУ�ƻ���һ�鳤Ϊ20m����Ϊ15m�ij����οյ�����һ����Ϊa��m�����������µIJ��������ƺ�����̵أ�
��1���������Ϊ�� ��m2���̵ص����Ϊ�� ��m2���ú�a�Ĵ���ʽ��ʾ����
��2����֪ij����˾�������̵ص����W1��Ԫ����W2��Ԫ���������S֮��ĺ�����ϵ��ͼ2��ʾ�����ֹ�˾��һƽ���������̵ص���۷ֱ�Ϊ�� ��Ԫ���� ��Ԫ����ֱ��д�����������W1��Ԫ�������̵ص����W2��Ԫ����a��m���Ĺ�ϵʽ�������ѧУ�����ɸù�˾�н�����Ŀ����Ҫ�����������Ȳ�����2m�Ҳ�����5m����ô����Ϊ����ʱ�����������̵ص��������ͣ���������Ϊ����Ԫ��
���𰸡���1��15a����300��15a������2���٢�80��70������W1��80��15a��1200a��W2��70��300��15a������1050a+21000��������Ϊ2��ʱ�����������̵ص��������ͣ���������Ϊ21300Ԫ��
��������
��1������ͼ�μ�����⣻
��2�����ֹ�˾��һƽ���������̵ص���۷ֱ�Ϊ![]() ��80Ԫ��
��80Ԫ��![]() ��70Ԫ�ڸ������⼴���г���ϵʽ����W��W1+W2��1200a+����1050a+21000����150a+21000���ٸ���2��a��5�����ɽ������.
��70Ԫ�ڸ������⼴���г���ϵʽ����W��W1+W2��1200a+����1050a+21000����150a+21000���ٸ���2��a��5�����ɽ������.
�⣺��1���������Ϊ15am2���̵ص����Ϊ��300��15a��m2��
�ʴ�Ϊ��15a����300��15a����
��2�����ֹ�˾��һƽ���������̵ص���۷ֱ�Ϊ![]() ��80Ԫ��
��80Ԫ��![]() ��70Ԫ��
��70Ԫ��
��W1��80��15a��1200a��
W2��70��300��15a������1050a+21000��
�����������Ŀ���ܷ���ΪWԪ��
��W��W1+W2��1200a+����1050a+21000����150a+21000��
��k��0��
��W��a�����������
��2��a��5��
�൱a��2ʱ��W����Сֵ��W��Сֵ��150��2+21000��21300��
������Ϊ2��ʱ�����������̵ص��������ͣ���������Ϊ21300Ԫ��
�ʴ�Ϊ����80��70��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϣ������ɸ���ȫ��ͬ��С������ѳɵ�һ��������![]() ����ͼ��ʾ.
����ͼ��ʾ.

��1���뻭�����������![]() ������ͼ.
������ͼ.
��2�������˼�����![]() �ı������Ϻ��ᣨ���������ϵ�һ�治�磩�������������Ǻ�ɫ��С��������_______��.
�ı������Ϻ��ᣨ���������ϵ�һ�治�磩�������������Ǻ�ɫ��С��������_______��.
��3�������������ͷ����һЩ��ͬ��С������������ڼ�����![]() �ϣ�Ҫ��������ͼ������ͼ���䣬������������________��С������.
�ϣ�Ҫ��������ͼ������ͼ���䣬������������________��С������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1����ABC�У�![]() ��AB�Ĵ�ֱƽ���߽�AC�ڵ�D������BD����AC=2��BC=1������BCD���ܳ�Ϊ ��
��AB�Ĵ�ֱƽ���߽�AC�ڵ�D������BD����AC=2��BC=1������BCD���ܳ�Ϊ ��
��2��OΪ������ABCD�����ģ�EΪCD����һ�㣬FΪAD����һ�㣬����EDF���ܳ�����AD�ij���
����ͼ2��������EDF��Ҫ�߹���ͼ����д������������ͼ�ۼ�����
����ͼ3�в�ȫͼ�Σ���![]() �Ķ�����
�Ķ�����
����![]() ����
����![]() ��ֵΪ ��
��ֵΪ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����֪��A��2a2+3ab��2a��1��B����a2+ab��1��
��1����2A��3B��
��2����A+2B��ֵ��a��ȡֵ�أ���b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ּ�ʱ��������0��00ʱ�̵�ȼ����������ʣ��ij���h��cm����ȼ�յ�ʱ��x��h��֮����һ�κ�����ϵ��h��x��һ���Ӧ��ֵ�����ʾ��
ȼ�յ�ʱ��x��h�� | �� | 3 | 4 | 5 | 6 | �� |
ʣ��ij���h��cm�� | �� | 210 | 200 | 190 | 180 | �� |
��1��д����������0��00ʱ�̵�Ȼ����ʣ��ij���h��cm����ȼ��ʱ��x��h���ĺ�����ϵʽ�������ͺ�������ʽ��x��ϵ�����������ʵ�����壻
��2��ͨ������˵����������ʣ��ij���Ϊ125cmʱ��ʱ�̣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
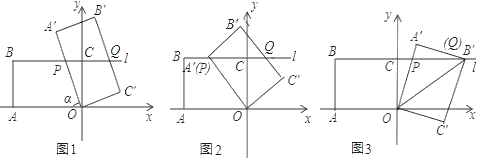
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��A����4��0����ֱ��l��x�ᣬ��y���ڵ�C��0��3������B����4��3����ֱ��l�ϣ�������OABC�Ƶ�O��˳ʱ�뷽����ת���ȣ��õ�����OA��B��C������ʱֱ��OA����B��C���ֱ���ֱ��l�ཻ�ڵ�P��Q��
��1��������90��ʱ����B��������Ϊ�� ����
��2����ͼ2������A������l��ʱ����P������Ϊ�� ����
��3����ͼ3��������OA��B��C���Ķ���B������l��ʱ��
����OP�ij��ȣ���S��OPB����ֵ���� ����
��4���ھ���OABC��ת�Ĺ����У���ת��0��������180��������O��P��B����QΪ������ı����ܷ��Ϊƽ���ı��Σ�����ܣ���ֱ��д����B���͵�P�����ꣻ������ܣ����Ҫ˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�������� A��B �����Ӧ���ֱ�Ϊ��4��20��
��1���� P ��Ϊ�߶� AB ���е㣬�� P ���Ӧ������
��2������ A���� B ͬʱ�ֱ��� 2 ����λ����/����ٶ������˶����� M��M ����ԭ�㣩ͬʱ�� 4 ����λ����/����ٶ������˶��������� M ���� A���� B �ľ�����ȣ����ʱ M ��Ӧ������
��3���ڣ�2���������£��Ƿ���� M �㣬ʹ 3MA=2MB�������ڣ������ M ��Ӧ�������������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
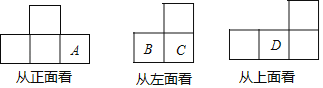
����Ŀ��һ���������ɴ�С��ͬ��С�������ɣ������������ļ��������״ͼ��ͼ��ʾ��
��1����A��B��C��D��4������λ���ϵ�С������ĸ�����
��2��������������ɶ��ٿ�С��������ɵģ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���е������μ����õ�ͼ�ڣ�ͼ���й���4�������Σ���ͼ����һ�������μ����õ�ͼ�ۣ�ͼ���й���7�������Σ���ͼ����һ�������μ����õ�ͼ�ܣ�ͼ���й���10�������Ρ��������ȥ�����2014��ͼ�й��������εĸ���Ϊ( )
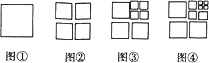
A. 2014. B. 2017 C. 6040 D. 6044
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com